Why is “water takes the steepest path downhill” a common approximation?

Question

Googling around, I see people saying that water takes the steepest path downhill. Of course, this is just an approximation. Things like inertia, friction, etc. will cause deviations. I’m curious about why this is a good approximation to begin with. Are there a collection of hypotheses we can make about a drop of water from which it can be derived that water will take the steepest path downhill? One of these assumptions should be “no inertia”, but I’m not sure how to express that mathematically exactly.

To be more mathematical about it, suppose we have a mountain defined by some smooth map $f:\mathbb{R}^2 \rightarrow \mathbb{R}$. If $p(t)$ denotes the location of the drop of water projected down to the $xy$-plane at time $t$ from some starting point, we see that $$\frac{d^2}{dt^2}p \propto - \nabla_p f$$ But the curve of steepest descent would be $$\frac{d}{dt}p \propto - \nabla_p f$$ Is there a way to make assumptions about the drop of water such that the first equation reduces to the second?

Some authors online simply assume that water flows as to minimize its potential energy as quickly as possible, but it’s simply asserted.

Answer 1

One way to understand "ignoring inertia" is this: aside from gravity and the surface normal force, there are various friction-like forces: viscosity, turbulence, drag with the surroundings. Think of a river after a waterfall:

Within the waterfall, the water acquires a lot of kinetic energy, so you would expect it to "remember" that and continue in its direction, even if it didn't lead in the direction of steepest descent. However, in the whitewater region under the waterfall, much of that kinetic energy is converted to heat energy and the water becomes quite still very soon. Then it is again pushed in the direction of steepest descent.

This means that the effect of inertia is short-lived and can be neglected over long distances.

The way to formalise this would be by adding a viscosity/friction term to your first equation, making it:

$$ \frac{\mathrm{d}^2 p}{\mathrm{d} t^2} \propto - \nabla_p f - \lambda \frac{\mathrm{d} p}{\mathrm{d} t} $$

Then, assuming $\lambda$ is high, most of the time $\frac{\mathrm{d} p}{\mathrm{d} t}$ will be proportional to the applied force. It also shows where this approximation fails: when $\nabla_p f$ changes rapidly (such as immediately under a waterfall), there is a transitional period (water splashing everywhere around).

Answer 2

Why is “water takes the steepest path downhill” a common approximation?

... One of these assumptions should be “no inertia”, but I’m not sure how to express that mathematically exactly.

... $$\frac{d^2}{dt^2}p \propto - \nabla_p f$$ ...$$\frac{d}{dt}p \propto - \nabla_p f$$

...I understand why the force vector points downhill. I also understand that this is an approximation. However, it’s stated all over the web that water generally follows the steepest path downhill if we ignore inertia.

In hydrodynamics the term "inertial force" or "inertial forces" refers to the part of the equation of motion that looks analogous to $$ ma\;, $$ in classical mechanics of point particles.

In hydrodynamics we end up using this term "inertial" analogously because $m$ is the "inertial" mass.

For example, the Navier-Stokes equation for a fluid flow velocity $\vec u$ looks like $$ \underbrace{\rho\left(\frac{\partial \vec u}{\partial t} + \vec u\cdot \vec \nabla \vec u \right)}_{inertial\;part} = \mu \nabla^2\vec u - \vec \nabla P - \rho\vec\nabla \phi \;,\tag{1} $$ where the left-hand side is the "inertial part," and the first term on the right is the viscous part, the second term on the right is due to the fluid pressure, and the last term on the right is the density times the gradient of the potential energy (analogous to something proportional to gradient of the function $f(x,y)$, in your question, since in your case the potential is gravitational pointing in the z direction, and so is proportional to $f$.)

You see that the only derivative of the fluid velocity with respect to time is in the inertial part of Eq. (1).

So, roughly, and ignoring the pressure, when the inertial part dominates we have: $$ \frac{du}{dt}\sim -\nabla \phi \tag{2} $$

And, again roughly, and ignoring the pressure, when the inertial part can be ignored we have: $$ \nabla \phi \sim \frac{\mu}{\rho L^2}u\;, \tag{3} $$ where $L$ is some average length scale for the fluid that I used to replace the spatial derivative of the velocity in this rough approximation.

If we write $$ u\propto \frac{dp}{dt} $$ then my Eq. (2) looks analogous to your first equation, and my Eq. (3) looks analogous to your second equation.

Answer 3

From your comments it seems that your issue is with the 'ignoring its inertia' requirement. One way to ignore inertia (approximately) would be to imagine that every fraction of a second the body of water under consideration is momentarily halted (i.e. its velocity reduced to zero by some mysterious external influence)> It then has zero inertia and as a result of the combination of gravity and normal forces from the surface it is sitting on, it will be accelerated in the direction of steepest decent - thus the waters average velocity before it is stopped again would be in the direction of steepest decent. In that scenario, the water would very nearly (and very slowly) follow the path of steepest decent.

In a more realistic scenario the water is never stopped, but friction against the bed of the stream and viscosity in the water results in a frictive force that opposes the existing motion of the water, i.e in a direction opposite its direction of flow. As a result the water never accelerates to a particularly high velocity and its momentum is always kept in check. Excluding times when it is in free-fall, for example after dropping off a water-fall, the water will 'flow' much more slowly than a frictionless object would and its direction of motion will be dominated by local forces/accelerations.

If you take the limit of very high friction and viscosity, for example a flow of honey down the hillside, its velocity will always be near zero so its momentum can be almost completely 'ignored' in determining the path down the hillside. The honey woul dvery nearly follow the steepest decent line at all times.

If you took a material with zero friction and viscosity (for example a flow of perfectly smooth and elastic ball bearings) then the 'fluid' woul dcontinue to accelerate, its momentuum woul dcontinue to grow and you could not 'ignore' the momentum in determining the path of flow. That material would likely follow a path far from the simple steepest decent.

Water is intermediate between these, but in practice the friction and viscosity has a significant effect in slowing down water flow (you don't see mountain streams flowing at many tens of metres per second in for example). So to a first approximation, you can ignore teh water's momentum in predicting where it will flow.

Answer 4

Note: We should be clear about what is meant by "steepest path". In the diagram below, there are two possible paths. They both drop by the same amount over the same overall distance, so they technically have the same average steepness. However, we can make a distinction by defining the "steepest path" as being the path with the greatest initial gradient immediately downstream of the location under consideration.

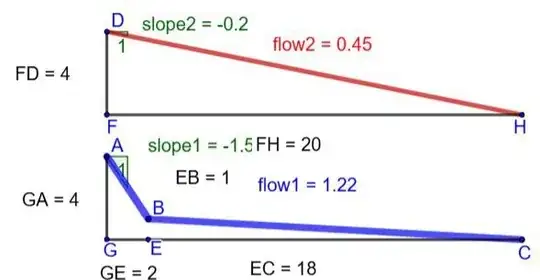
In the diagram, blue and red paths represent two open channel viaducts with identical surface roughness, water cross sections and initial head heights. Interestingly, the flow in the blue path is approximately $3$ times as much as the flow in the red path, even though the red path has the straightest path and the lowest total path length. The final section of the blue path has a shallow slope, but this can be compensated for by making that section wider. That section could be a natural river with gently rising banks that can accommodate the extra flow. Note that the flow in the blue path is greater than the flow in the red path, even though the head difference in the steep part of the blue path is only $3$ units, and the total head difference of the blue path is $4$ units.

I think this question can initially be analysed by using an electrical circuit analogy and then return to the geological case with water flow in a landscape, which obviously has some differences. Consider a simple circuit with a $12 \ \text{V}$ battery and two resistors ($\text{A}$ & $\text{B}$) in parallel, where $\text{A}$ has a resistance of $3 \ \Omega$ and $\text{B}$ has resistance of $6 \ \Omega$. The total resistance is given by the equation: $$R_{\text{AB}} = \frac{R_{\text{A}} R_{\text{B}}}{R_{\text{A}}+R_{\text{B}}} = \frac{18}{9} = 2 \ \Omega.$$ From this the current through both resistors is $$I_{\text{AB}} = \frac{V_{\text{AB}}}{R_{\text{AB}}} = \frac{12}{2} = 6 \ \text{A}.$$

The current through resistor $\text{A}$ is $$\frac{V_{\text{AB}}}{R_{\text{A}}} = \frac{12}{3} = 4 \ \text{A}$$ and the current through $\text{B}$ is $$\frac{V_{\text{AB}}}{R_{\text{B}}} = \frac{12}{6} = 2 \ \text{A}.$$

It should be obvious that in this analogy, the electrical current represents the water current, and the voltage (or electrical potential) represents the height of the landscape at a given point. The $6 \ \Omega$ resistor can be thought of as two $3 \ \Omega$ resistors in series, and the drop in voltage across each resistor in the $\text{B}$ path is half the drop in voltage across the $\text{A}$ resistor, so the $\text{B}$ path can be thought of as less steep than the $\text{A}$ path. (The drop in potential per unit length of the resistor is lower.)

The important thing to note here is that while most of the current goes through the resistor with the lowest resistance (and steepest path by analogy), not all the current goes through resistor $\text{A}$. So the expression "the current takes the path of least resistance" is not strictly true if by "the current" we mean all the current. If all the current only flowed through resistor $\text{A}$ (the path of least resistance), the total current around the circuit would be only $4 \ \text{A}$. It appears that rather than taking the path of least resistance, the current takes all available paths in order to maximise the total current flow per unit time.

Now, back to the case of a river in a real landscape. Imagine we have a river flowing directly South. It flows into a lake where there is a natural dam preventing the river from continuing South. (The South directed momentum of the river is no longer a factor due to this barrier) Let's say that two rivers flow out of the lake to the East and the West, and the river to the East goes down a steeper slope, so the flow through the East River is greater than the flow in the West River. One factor that has not been taken into account so far is erosion. The faster flow in the East River causes a greater degree of erosion in the East River, making it get wider and deeper faster than the West River. This increases the flow in the East River even more, and it tends to drop the level of the lake. The drop level in the lake might drop below the depth of the West River, cutting the flow off completely in the West River so that the final route of the total river is via the steeper East route. Erosion is the key factor in the fact that real rivers in a real landscape tend to end up taking the steepest route. If a river happens to split into two paths, and one path is over hard rock, and the other path is over soft rock, the soft rock will erode faster, making that path deeper and wider until all the water ends up flowing down the steeper path created in the soft rock.

==============================================

I get the impression the OP is more interested in a more abstract mathematical interpretation than a practical, real-world scenario with real-world complications like erosion. Consider a drop of water on an inclined hydrophobic plane. We could consider the extreme where the plane is vertical. The question becomes: why does the water droplet go straight down and not horizontally or upwards? Intuitively, the answer seems obvious, and, informally, if there is a gravitational potential field, we can assign a gradient vector to every point in the field, and the particle will always be accelerated in the direction of the gradient that goes from a higher potential to a lower potential, but its actual future trajectory will also depend on its current velocity. If the droplet has a significant initial horizontal velocity of $\dfrac{\mathrm{d}x}{\mathrm{d}t}$ and the force of gravity is accelerating the droplet in the $y$ direction, its velocity vector rotates more towards the downhill's $y$ direction over time. If there is resistance and $\dfrac{\mathrm{d}x}{\mathrm{d}t}$ gets smaller over time, the velocity vector rotates even faster to the downhill's $y$ direction. Since the OP has asked us to ignore inertia, $\dfrac{\mathrm{d}x}{\mathrm{d}t}$ goes to zero, and the only possible velocity vector is straight downhill.

More formally, the answer is that the drop takes the path of least action. Briefly, if we consider different paths the droplet could take to get from $\text{A}$ to $\text{B}$, the action ($S$) of any given path is equal to the integral of the Kinetic Energy minus the integral of the Potential Energy with respect to time. To find the KE and PE as functions of time, we first need the equations of motion for distance (which I will use for height) and for velocity. They are:

$$h = v_0 t - \frac{1}{2} g t^2 \quad \text{and} \quad v=v_0 + g t.$$

The equations for $\text{PE}$ and $\text{KE}$ are:

$$\text{PE} = mgh \quad \text{and} \quad \text{KE} = \frac{1}{2} m v^2.$$

Substituting the equations for $h$ and $v$ as functions of time into the equations for $\text{PE}$ and $\text{KE}$ gives:

$$\text{PE}(t) = mg \left(-\frac{1}{2} g t^2 \right) = -\frac{1}{2} m g^2 t^2 \quad \text{and} \quad \text{KE}(t) = \frac{1}{2} m (g t)^2 = \frac{1}{2} m g^2 t^2.$$

I have left out $v_0$ as I will use an initial velocity of zero for the water droplet. This simplifies things a lot.

Now we find the action:

\begin{align} S &= \int\limits_0^t \text{KE}(t) \ \mathrm{d}t - \int\limits_0^t \text{PE}(t) \ \mathrm{d}t \\ &= \int\limits_0^t \left(\frac{1}{2} m g^2 t^2 \right) \ \mathrm{d}t - \int_0^t \left(-\frac{1}{2} m g^2 t^2 \right) \ \mathrm{d}t \\ &= \frac{1}{3} g^2 m t^3. \end{align}

Any other path would yield a higher value of $S$.

Calculating $S$ for diagonal paths is more complex. For the vertical, inclined plate and a non-vertical path, the equations for a projectile trajectory and an initial non-zero velocity would be required. For an inclined plane, the cosine of the gravitational acceleration factor would have to be used.

Answer 5

Expanding on @Aliens answer, acceleration gives the change in velocity over time. Velocity in turn is the change in position over time. Since the force, and therefore acceleration, is always changing the velocity towards the steepest change in height, the change in position is driven along the steepest path down.

If you want a perhaps more "fundamental" picture of why a particular path is followed in physical systems, look up the principle of least action.

Answer 6

Water flows across a surface due to the normal force from the surface. The normal force from an angled surface can be decomposed into the horizontal and vertical components. The horizontal component determines which way the water flows. This horizontal component of the normal force always points directly downhill - the force accelerating a drop of water at any point is always accelerating it directly downhill. The drop may move in other directions if it already has velocity, but water on a slope can't accelerate in any direction other than downhill.

Answer 7

Water takes the steepest path only when you ignore inertia. It's because the gradient of potential energy is force. So the velocity is not in the same direction as the height gradient but acceleration is.

Answer 8

In your question you focus on droplet. In reality it's got little or nothing to do with a single droplet. A single droplet would be extinguished very early on.

Initially the water would take a few paths approximating to the steepest path. Factors such as surface tension, absorbtion, temperature surface rugosity etc would be important.

The earliest paths would not be the steepest, as time elapsed the flow of water would increasingly find the steepest most direct path.

Elapsed time would be an important early parameter. Flow rate and other dynamic properties of the situation would be important.

After a while the flow path, we could write:

path = fn(gravity, inertia, random chaotic component, deflection and tumble, temperature, surface tension).

Now how to model this, crucially the factors which retard flow have to be understood, you cannot ignore inertia. Like the executive toy momentum is transferred (in this case reflected back) why not build a model and introduce random inertia/momentum events.

The mechanisms that retard flow have to be understood, without them the flow would reach infinite velocity. I suspect that inertia/momentum is not the only mechanism.

Earlier I read the answer that suggests analogy of an electric circuit, not seeing this as a good analogy, water is incompressible - no inductive or capacitive elements, resistance as in flow restriction is incomplete.

This is a fascinating problem I hope you solve it and end up with an equation that is a very close approximation to the real situation.

Answer 9

The statement "water takes the steepest path downhill" is a common approximation based on the principle of gravitational potential energy. When water flows, it naturally moves towards areas of lower potential energy, which generally means it follows the path of greatest slope. This is because:

Gravity: Water is pulled downward by gravity, so it naturally seeks out the steepest descent to reach lower elevations quickly. Energy Minimization: The flow of water tends to minimize its potential energy. The steepest path downhill allows it to achieve this goal most efficiently. Flow Dynamics: In natural systems, the path of steepest descent often corresponds to the most direct and fastest route for water flow, reducing resistance and increasing efficiency. This principle helps in various fields, such as hydrology and geography, to model water flow and understand drainage patterns.

Answer 10

Two ideas to understand.

First, Nobel Lauriat Kip Thorne referred to Einstein's Law of Time Warps. He said "Things like to live where they age the most slowly. Gravity pulls them there." So we understand that things always move to where time runs more slowly - that is towards the base of your mountain.

Second, you'll find that gravity works exactly like a low pressure system - a pressure system in time. It is this pressure of time from any point "B" above the planet, compared to the pressure of time of a point higher "C" or lower "A" (You could say greater gravitational potential "C" and lower gravitational potential "A" to use scientific jargon.)

Now, look at this air bubble inside a water ball on the ISS in space.

The air bubble stays in the middle of the water ball exactly because the pressure is the same all around the air bubble. But what if you could somehow reduce the pressure on one side of the water ball? Then the air bubble would immediately move to that side and escape the water ball.

Now imagine that you could reduce the pressure all around the air bubble, but by different amounts. Reduce it by 10% on the right side; 20% on the left side; 20% on the top and 40% on the bottom. You can see that the air bubble will move towards where the difference is greatest, that is towards the bottom where there is at least a 20% pressure differential from any other direction.

So why does your water fall on the steepest part of the mountain? The answer is because that is where the pressure differential in time is greatest from what is on top of the water compared to below the water. In other words, the gradient of time is greatest where the mountain is steepest.

It all has to do with gravitational time dilation. In your mathematical calculations simply make a graph of the differential in time dilation on every possible path above and below the water all along the circumference of the mountain. Obviously the water cannot flow if it is blocked by a rock, but most follow one of many potential channels. You can see that the water will move to the channel of greatest time differential.