David J. Griffiths Introduction to Electrodynamics page 456 shows the following figure:
... then page 461:
... and page 462:
The following thought experiment has three electrons, negative charges, in an intergalactic space observed from $Q_1$, $Q_2$ rest frame $K$:
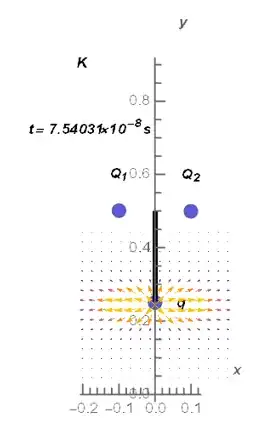
The charges $Q_1$ and $Q_2$ are 'almost stationary' held by a device in $K$ reference frame, the charge $q$ accelerates straight down along the $y$ axis in $-y$ direction. This is an isolated system. The figure above shows the electric field as observed from electron accelerated momentarily comoving inertial frame (MCIF) in $K$ frame at the time $t=7.54031\times10^-8s$ and the position $\{0,0.25,0\}$ in meters. The isolated system is being observed from a moving inertial frame $K'_1$:
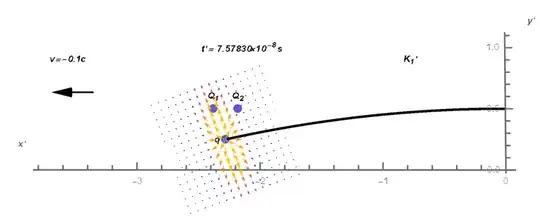
The figure above shows the electric field as observed from MCIF that is tangent to the accelerated electron trajectory in $K'_1$ inertial frame at the time $t'=7.5783\times10^-8s$ and the position $\{-2.27192, 0.25, 0\}$ in meters. Note: The flattened field is not correlated to the speed, it is bigger for the demonstration purpose.
Question: How do we transform the EM field from $K$ to $K'_1$? Is it safe to use equations (10.75), (10.76) in any inertial reference frame without any other considerations?
Edit 2024-08-01:
A new question arises, what does the frame dependent field mean for the Lorentz force?
David J. Griffiths Introduction to Electrodynamics page 460:
The charge $q$ repels $Q_1$ and $Q_2$ symmetrically in $K$ reference frame but the repulsion is not symmetrical in $K'_1$ reference frame. The Lorentz force has bigger magnitude between $qQ_1$ compared to $qQ_2$ in $K'_1$ frame. The isolated system body is not torqued in $K$ but it is torqued clockwise in $K'_1$ frame. The $q$ EM field 'rotates' counterclockwise in $K'_1$ and the conservation of angular momentum 'rotates' the isolated system body clockwise.
Angular momentum has two parts orbit and spin/rotation. Orbit is frame dependent but the direction of the spin/rotation is absolute.
Question: Is prediction of no spin/rotation of the isolated system body in $K$ and prediction of clockwise spin/rotation of the isolated system body in $K'_1$ a contradiction to special relativity?
Edit 2025-01-15:
The equation (10.74) works in any inertial reference frame. All the input factors have to be evaluated at the retarded time. When the simultaneity changes between the moving inertial frames that is the process/mechanism how/why the equation (10.74) can work in any inertial reference frame.
The charge $q$ is emitted at the event $\{t,x,y,z\}=\{0,0,0.5,0\}$ of the rest frame $K$. The dimensions are $\{[s],[m],[m],[m]\}$. The charge accelerates at $8.7941 \times 10^{13}m/s^2$ in $-y$ direction for approximately $3.33564 \times 10^{-10}s$. The retarded time is $4.9 \times 10^{-43}s$ according to software I use, very close to $0$, the start time of the emission of the EM field from $q$ towards charges $Q_1, Q_2$. The time is synchronized between $q, Q_1, Q_2$ charges and it is the same time $3.33564 \times 10^{-10}s$ when the first $q$ photons hit $Q_1, Q_2$. The charge $q$ will accelerate to location $\{0,-0.5,0\}$ where it is going to be absorbed. We will integrate the Lorentz force $F$ over the time of the acceleration to compare the impulse between $qQ_1$ and $qQ_2$.
The total time for the charge $q$ to reach $\{0,-0.5,0\}$ is $1.508 \times 10^{-7}s$. The integration will be done in a software with splitting the full time into small steps. Smaller steps are better because the calculation will be more precise. Here is an example of one calculation in the rest frame $K$:
Here is an example of one calculation in the frame $K'_1$
$K$ frame impulse in $y$ axis direction is equal for charges $Q_1, Q_2$ but it is not equal for $K'_1$ frame. The calculations show how the isolated system body is being torqued in the $K'_1$ frame. The contradiction of observed clockwise direction of spin/rotation in $K'_1$ frame compared to no spin/rotation in the $K$ frame challenges our understanding of the special relativity.
Conservation of linear momentum in the rest frame $K$.
The Lorentz force acting between the $q,$ $Q_1,$ $Q_2$ charges through the EM field is continuous. The conservation of linear momentum holds in every tiny $dt$ moment. The barycenter of the isolated system is inertial and located at the origin of the rest frame. The bottom part of the isolated system has bigger mass with one extra electron after the absorption at the end, that means the isolated system shifted a small $dy$ in the $+y$ direction to compensate and to keep the barycenter inertial. No more motion of the system is expected after the absorption.
Conservation of momentum in $K'_1$ frame.
The isolated system is being torqued in the $K'_1$ frame as per the calculations above and the rotation of the system starts. When the electron $q$ charge is absorbed then the conservation of the angular momentum holds and there is no force acting to stop the rotation. The system will flip after 'long time'. The $Q$ charges will be at the bottom and the $q$ charge at the top. The rotation/flipping would not stop due to conservation of the angular momentum.
If the above analysis is correct then the trouble starts...
... to be continued ...