2

On reading up about the bounce solution for false vacuum decay in S. Coleman's The Fate of the False Vacuum I it was stated that the equation $$0 = \frac{1}{2} \frac{\partial q}{\partial \tau} . \frac{\partial q}{\partial \tau} - V(q)\tag{2.12}$$ necessarily implies that there is no stable equilibrium point. I understand this as if $\partial q/\partial \tau = 0$ then we must have $0 = -V$, so there is no equilibrium as long as there is a finite potential. They then state that the classical equilibrium point can be reached asymptotically as the limit of $q$ as $\tau$ tends to minus infinity. There have so far been no assumptions that the potential tends to 0 at infinite time. Should this have been assumed or is there (more likely) something I'm misunderstanding?

Qmechanic
  • 220,844
Adam P
  • 359

1 Answers1

2

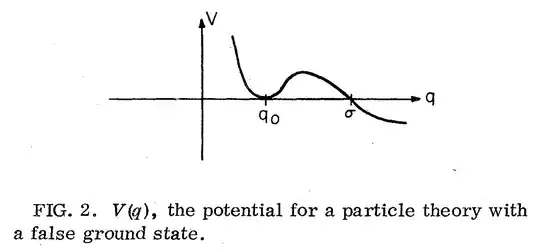
  1. For the shape of the potential $V$ Ref. 1 is apparently referring to Fig. 2, i.e. the potential $V$ is assumed to have classical false vacuum, i.e. a local minimum $V(q_0)=0$ that is metastable, i.e. not a global minimum. Assuming $V$ is continuous, there must be another point $\sigma$, where $V(\sigma)=0$.

    Fig. 2

  2. Ref. 1 next considers a bounce/an instanton between $q_0$ and $\sigma$. Concerning its duration in Euclidean time, see e.g. this related Phys.SE post.

  3. For more information, see e.g. this related Phys.SE post.

References:

  1. S. Coleman, Fate of the false vacuum I: Semiclassical theory, Phys. Rev. D15 (1977) 2929, Erratum Phys. Rev. D16 (1977) 1248.
Qmechanic
  • 220,844