A paradox while explaining the equilibrium of books

Question

An even number of books (say four) are held in the manner shown in the figure. It is obvious that if we apply a large force inwards, we can increase the normal force, and hence the friction which keeps the books in equilibrium. Assume all the books are identical.

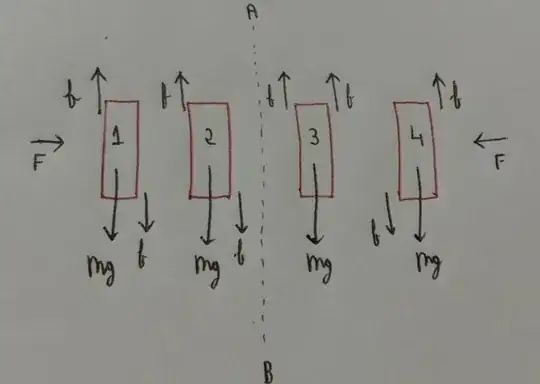
On considering the equilibrium of the books individually, two problems arise when showing the direction of friction acting on the books two and three. (consider figure)

F denotes force applied and f denotes the friction force between the books which may or may not be same between all the books.

The problems:

1. The situation is symmetrical about the line AB hence, the free body diagram on the left side of AB must be same as that on the right side of AB.

Thus the friction between the book 2 and 3, I believe, must act in the same direction. However such a thing would violate Newton's third law that friction must act in opposite directions on the two surfaces in contact.

2. Neglecting the fact that the situation is symmetrical (as I have done in the figure), equilibrium is not possible for both the books 2 and 3 simultaneously as the net upward force balancing weight for both is different.

My questions:

1. Am I doing something horribly wrong?
2. Does it mean that no friction acts between books 2 and 3?

NOTE: Such a problem arises only when even number of books are involved.

Answer 1

You are correct, in a scenario with an even number of books there will be no friction acting between the pair in the middle. To see this, take the simplest case - two books. The force $F$ applied by the hand gives rise to a frictional force $f_1$ between the hands and the books they are touching. This friction force $f_1$ is equal to the weight of each book, given that $F$ is large enough for the surfaces. Since the books do not have a tendency to move with respect to each other (if $F$ were taken out, they'd fall together!), there is no friction between them.

For more than 2 books (say 4, as in your question), everything outside the middle two books acts just like the hands in the 2-book case. However, for the outer books, there is a different for $f_2$ acting between them and the hands (i.e hand to outer book is $f_2$ and outer book to middle is $f_1$ with $f_1 = mg$ and $f_2 = 2mg$). You can verify that the directions of the forces match to make the net force on each book zero.

P.S The symmetry argument you present is a pretty slick way to show that no friction acts between the middle two books. Avoids all the arrows and head-scratching :)

Answer 2

Not all friction forces labeled $f$ in the sketch are identical. I fact, they become smaller as you move towards the centre on the stack. Realizing this removes all of the mentioned issues.

• The frictions between the hands and the outer books are large. Essentially, these carry the total weight of all four books.

• The friction between books 1 and 2 as well as between 3 and 4 are smaller. These carry only the weight of books 2 and 3.

• There is no friction between books 2 and 3. There is nothing for such a friction force to carry.

The friction forces do appear in opposite force pairs everywhere as per Newton's 3rd law, but you should sketch them progressively smaller towards the centre of the stack. Now there is no symmetry issue, no violation of Newton's 3rd law anywhere, and a clear explanation of the purpose of each friction force.

• E.g., the friction from book 1 on book 2 points upwards and equals the weight of book 2.
• In turn, book 2 pulls down in book 1 with this same friction force, which is the weight of book 2. The friction force from the hand on book 1 must carry the weight of book 1 as well as counteract this friction from book 2 (which all in all means that it carries the weight of both books).
• The farther from the centre you are in the stack, the more the friction forces have to carry.

All in all, be careful not to be "too quick" when subdividing a system into split systems. My advise would be to treat each split system individually and to avoid drawing a combined sketch. In your treatment of each split system you will apply boundary conditions and "effects", which here are constituted by the friction forces. Be very careful with any assumptions on boundary conditions - in fact, try to forget any external information until you have drawn out the full freebody diagram for a split system so as to avoid applying assumptions that only applied to the full system.