4

I cannot indicate an error in the following reasoning if it is done in the framework of classical physics.

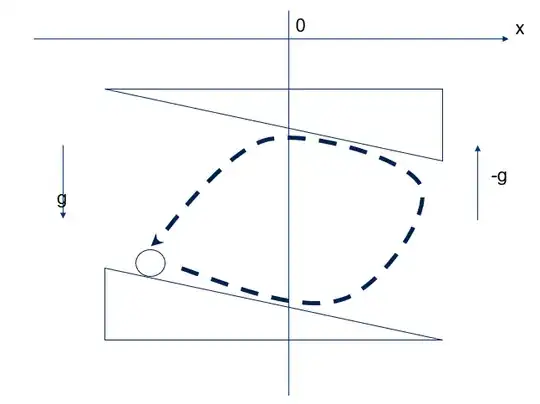
Diagram

Let's make the imaginary setup with two wedges and the ball, when the gravity in the left and right half-spaces is anti-parallel, namely:

$$g(x)=\begin{equation} \begin{cases} g, x \le 0\\ -g, x > 0 \end{cases}\,. \end{equation}$$

Let's put a ball on the lower wedge. Then, when released, the ball to the left starts to accelerate indefinetetly (dashed line), repeating the cycle.

I am aware that such a configuration of gravitational fields is impossible to create. From theoritical point of view I suspect there are some limitation by general relativity that the gravitational field should be smooth as well as such a system will start to emit strong gravitational waves losing energy and finally it will stabilize in some equilibrium.

But if we take classical physics what is it violated in such a configuration?

Artem
  • 242

2 Answers2

16

If we let the $y$-axis point upwards then OP's 2D gravitational field is $$\vec{g}~=~ \begin{pmatrix} 0 \cr g~{\rm sgn}(x)\end{pmatrix}.$$ It has a non-zero curl $$(\vec{\nabla}\times \vec{g})_z~=~2g\delta(x),$$ and is hence not a conservative field.

Qmechanic
  • 220,844
5

The potential that yields your provided force field is discontinuous. One possible choice would be $$V(x,y) = \begin{cases} gy & x\leq 0 \\ -gy & x>0 \end{cases},$$ which has a dicontinuity at $x=0$ whenever $g>0$. Hence, the force in $x$-direction, i.e. $\partial_x V$ is not defined at $x=0$. You can solve Newton's equations only on one half of the anti-parallel gravitational system.

This is a purely mathematical argument. A physical argument would require a better (physically stable) model that yields a continuous potential. For instance: You could smoothen out $V(x,y)$ in $x$-direction introducing a large gradient around $x=0$. This will drastically slow down the particle at the transition point and ensure energy conservation.

Refik Mansuroglu
  • 507