Straight wire in moving uniform magnetic field induced emf

Question

My question is a follow-up to this one.

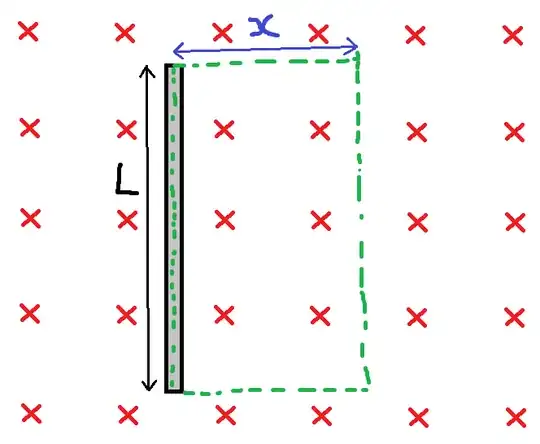
The green dotted line is the arbitrary loop which is constructed in the calculation of emf in the wire of length L. x is a variable which can be changed to alter the size of the loop. The red crosses are the flux density vectors of a uniform magnetic field.

In the linked question (Scenario 1), my understanding of the answer is:

1. Induced emf around a loop is equal to the rate of change of flux through the loop $\sum_{}^{}(t)$ with respect to time.
2. The flux through the loop is the surface integral $\phi_B = \iint_{\sum_{(t)}^{}}^{}\textbf{B}(t).d\textbf{A}$ . The induced emf $\varepsilon=-\frac{d \phi_B}{dt}$ (wikipedia faradays law of induction).
3. The loop path is arbitrary as long as it contains the straight wire i.e. the parameter x is arbitrary.
4. Because the loop is drawn in the diagram frame of reference and the wire is in motion, this means that the area of the loop is changing and therefore the flux through the loop is changing and an emf is induced.
5. No matter how large the parameter x is the rate of change of the loop area will be the same. Good.

Altering this scenario slightly - (Scenario 2) if the wire is held stationary in the diagram frame of reference and the source of the uniform magnetic field is now in motion moving to the left at constant velocity V. Following my logic from the steps above and drawing the loop still in the diagram/wire frame of reference:

1. The area of the loop of arbitrary size is not changing with respect to time.
2. The flux through the loop is not changing because the sum of all of the area elements dot product with the flux density is not changing with respect to time.
3. No emf is induced around the loop/in the wire.

My question is how does the surface integral form of faradays law arrive at an induced emf in this scenario? Is there some other relativistic affect which I have overlooked?

...

Sorry, I am going to sneak another closely related question on the end here. Imagine the wire and the source of the magnetic field are both stationary in the diagram frame of reference. Only the magnetic field is now changing in such a way that the flux density at every point in space is increasing linearly wrt time. (Scenario 3).

It makes sense to me that an emf is now induced in the wire since the flux through a loop which contains the wire is increasing with time.

My confusion lies in the way the loop is drawn. If we compare x=2 and x=4, then for x=4, at a given point in time there will be more flux through the loop and therefore the rate that flux changes wrt time will be larger and therefore there is a larger emf in the loop.

If using two different values of x will yield a different calculation of emf in the loop/wire then the selection of x cannot be arbitrary? Can anyone point out the point in my thought process where I am going wrong?

Thankyou in advance for any input.

Answer 1

First : scenario 1 and two are not the same in scenario 2 B moves relative to the full loop not only relative to the green rod, so there will not be any emf induced, same as if moving the whole loop relative to B. Third, yes the larger loop will have the larger emf, but why compare it to the previous cases? it isa different kind of changing the flux,

Answer 2

First, it is useful to make clear what EMF is. For any curve $\gamma$ (open or closed), it is $$ \mathscr{E} = \int_{\gamma} \mathbf E^* \cdot d\mathbf s, $$ where $\mathbf E^*(\mathbf x)$ is net impressed force per unit charge due to all causes, except due to conservative part of electric field (difference of potential does not contribute to $\mathscr{E}$), that would act on a test charge put at $\mathbf x$.

This EMF can have many contributions of different kind: a contribution $\int_{\gamma} \mathbf E_{i}\cdot d\mathbf s$ (due to induced electric field), a contribution $\int_{\gamma}\mathbf v\times\mathbf B_{ext}\cdot d\mathbf s$ (due to motional EMF, if the conductor moves in external magnetic field), or a contribution $\mathscr{E}_{bat}$ due to electrochemical processes in a battery.

When you use the Faraday law to calculate EMF in a closed path, you are calculating only those contributions that are due to induced EMF or motional EMF; this law says nothing about that kind of EMF (battery EMF is not connected to change of magnetic flux). The resulting EMF, in general, depends on the chosen path; it is not a property of the rod alone. In particular, it depends on whether a part of the closed path moves or is stationary.

In the first scenario, when part of the loop following the rod moves with the rod, and the rest of the loop is at rest, EMF in the loop equals EMF in the rod, because no other part of the loop contributes(because those parts do not move, and there is no induced electric field in this frame).

In the second scenario, where the rod is at rest, and the imaginary loop is at rest, magnetic flux does not change in time, so Faraday's law says EMF in the loop is zero. This is correct for this loop, stationary wrt to the rod. In the previous frame, this scenario looks as a moving rod and a loop of constant area that moves together with the rod - thus EMF is zero in both frames.

However, that does not mean that EMF in the rod (in contrast to the EMF in a closed path) is zero. The EMF in the rod does not depend on which path outside the rod is chosen to make up a closed path. In the first scenario, where the rod moves, the EMF in the rod is due to motional EMF, and has magnitude $BLv$. In the second scenario, in a frame where the rod is at rest, the EMF in the rod has the same value, but is due to electric field of the moving magnet.