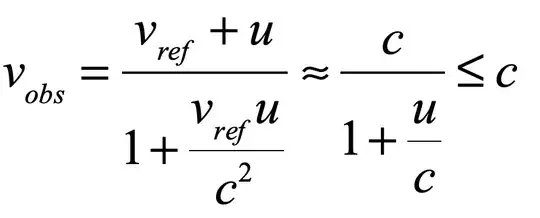Who will die first between two people on different spaceships, where both are in inertial frames?

Question

Here's something that's really been confusing me.

If two people on separate spaceships pass each other by, where both are in inertial frames, person A (on spaceship 1) could say that he is at rest and that person B (on spaceship 2) is the one moving, while person person A is at rest. But at the same time, person B could say that person A is the one moving while person B is at rest. This means that person A sees person B's time running slower, but at the same time, person B sees person A's time running slower. This means they are living in each others past.

But what if they are both the same age and are to die at the exact same age, and the exact same time (that is independent from them traveling on the spaceships). Person A would see person B age less then him, so person A would say that he is the one to die first. But at the same time person B sees person A age less then him, so person B would say that he is the one to die first.

From each others perspective the events of death that are supposed to occur at the exact same time, do not occur at the exact same time. The difference is the same for the both of them. But how is it possible that they see each other age less then them? it is as though they are living in each others past.

How is this allowed, and who is right?

I also believe that a third observer, situated perfectly in between person A and person B, so there speeds relative to this observer are the same, would see their death at the exact same time.

What are your thoughts on this?

As a side question, if two spaceships travel past each other at 0.8 times the speed of light, this is the same as one traveling at 2 x 0.8c or 1.6c past the other if it was at rest. But this is impossible because nothing can travel faster then the speed of light. how is this resolved?

Answer 1

In special relativity, the scenario you describe is a consequence of the relativity of simultaneity and time dilation. Both observers A and B will indeed see the other's clock running slower, which is not a contradiction but a result of their relative motion. The apparent paradox of simultaneous deaths occurs because events simultaneous in one frame aren't necessarily simultaneous in another. Each observer will see himself die first, but they can't directly compare experiences without one accelerating to join the other. A third observer equidistant from both would see the deaths as simultaneous. This doesn't violate causality because no information is exchanged faster than light. As for your side question, Einstein's velocity addition formula resolves the issue. I'd suggest taking a look at this page, which also includes example problems: https://phys.libretexts.org/Bookshelves/College_Physics/College_Physics_1e_(OpenStax)/28%3A_Special_Relativity/28.04%3A_Relativistic_Addition_of_Velocities

Answer 2

For different observers, there is no "absolute before" or "absolute after" of events occurring at different places. Time $t$ and space $\mathbf{r}$ are not absolute in special relativity, while their combination as 4-d event, $\underline{X} = (ct, \mathbf{r})$, is.

The biological time of an individual is its proper time $\tau$, i.e. time measured in its own reference frame.

It's not velocity (w.r.t what?) that influences proper time, while acceleration does: in the twin paradox, when the two twins meet after the trip, the youngest one is the one who has accelerated in his trip (and you can feel acceleration, and measure it with instruments).

So, while in general it's not possible to answer your question either as "before" or "after" due to the relativity of simultaneity, it's possible to say:

• Statistically, the expected age of death of two different individuals in uniform relative motion for their all lives, is the same when measured in their proper time.

• An observer in the middle point of the two individuals sees them dying at the same time, if their death are two events in space-time identified by the same value of the proper times of the dying people.