Do off-centre forces create additional energy?

Question

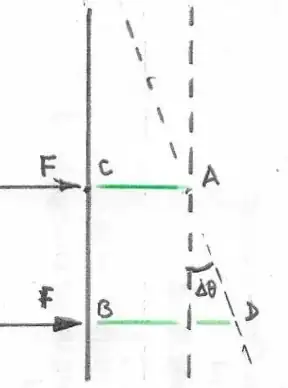
When a force is applied to a rigid body at its centre of mass, it accelerates. Over time, that acceleration becomes velocity, which gives the body a certain amount of kinetic energy.

However, if that same force were applied at the edge of that rigid body, perpendicular to the moment arm, it would also impart torque, leading to rotational energy as well as translational motion / kinetic energy.

In the second case (rotational + translational kinetic energy), it seems that more energy is present than in the first case (just translational kinetic energy). Yet, it's the same force, just applied to a different location on the body. How can this be?

I'm sure that I've misunderstood something, so clarification is appreciated!

Answer 1

If the line of action of the force is not through the centre of mass then body can be thought of as being acted on by a force whose line of action is through the centre of mass which produces a linear acceleration of the centre of mass and a couple which produces an angular acceleration of the body.

Thus work is done by the applied force displacing the centre of mass of the body and some extra work is done by the force because of the extra displacement due to the rotation of the body.

Where ever the force $F$ acts including at the centre of mass $C$ there is a displacement of the body, $CA$.

If the line of action of the force $F$ is not through the centre of mass the body also rotates about the centre of mass and so the displacement of the body is $BD$.
Because $BD>AB$ the force does more work when the line of action of the force is not hrough the centre of mass.

Answer 2

There is a standard demonstration in which an off-centre force is provided by a string wrapped around a cylinder on a air-table. Another string is connected to the c-of-mass of an otherwise identical cylinder. You pull both strings with the same force $F$, and see that the c-of-m's have the same acceleration. Meanwhile the string on the wrapped cylinder unwinds and the torque, $F\times$radius, makes its cylinder rotate. The unwindng means that you have move your hand through a much longer distance than for the straight-pull cylinder, so the work, $F\times$distance, is larger and provides the rotational energy.