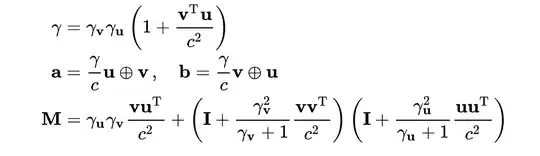An exercise asks one to show that given $v, u$ speeds much smaller than $c$ and oriented orthagonally, the composition of the lorentz boosts $B(\mathbf{v})B(\mathbf{u})B(\mathbf{-v})B(\mathbf{-u})$ is a rotation, and find the angle and direction of rotation.
Let $B(\mathbf{v})B(\mathbf{u})$ be written as $R(\mathbf{\epsilon})B(c\mathbf{a}/\gamma)$, and $B(\mathbf{-v})B(\mathbf{-u})$ as $B(-c\mathbf{b}/\gamma)R(\epsilon)$. Then the full product is $R(\mathbf{\epsilon})B(c\mathbf{a}/\gamma)B(-c\mathbf{b}/\gamma)R(\epsilon)$. If this is a pure rotation, then $B(c\mathbf{a}/\gamma)B(-c\mathbf{b}/\gamma)$ has to be a pure rotation, I don't see why this is.
Is the rotation aspect here the result of an approximation? In general, can you produce pure rotation through a product of boosts?(edit: yes from naturallyInconsistent's answer)
Doing it via. bruteforcing the matrix, I took the frame where $\mathbf{v}$ and $\mathbf{u}$ are aligned with the x and y axis respectively and got the following matrix for the spatial part of the transformation. Indeed $\mathbf{e_z}$ is an eigenvector and seems to be the axis of rotation, but I couldn't seem proceed to simplify it as $\gamma_v^2(1-\gamma_u^2v)$ goes to $1+v$ whilst $\gamma_u^2(1-\gamma_v^2u)$ goes to $1+u$ for small $u$, $v$. \begin{bmatrix} \gamma_v^2(1-\gamma_u^2v) & \gamma_v\gamma_uvu(\gamma_v+\gamma_u-\gamma_v\gamma_u) & 0 \\ -\gamma_v\gamma_uvu & \gamma_u^2(1-\gamma_v^2u) & 0 \\ 0 & 0 & 1 \end{bmatrix}
I am trying to find a $\theta$ s.t. this is equal to \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) & 0\\ 0 & 0 & 1\\ \end{bmatrix}
Is this what one would usually look for?