1

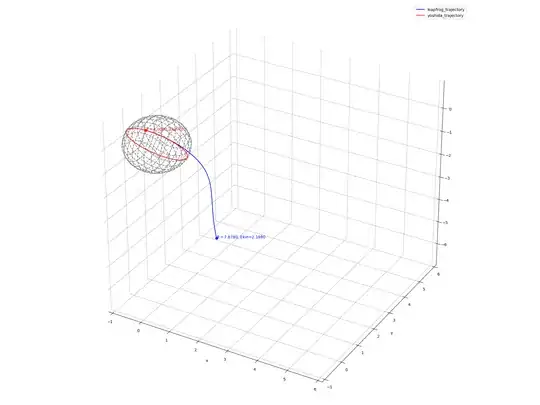
I was interested in demonstrating the notion of geodesics in constrained motion and prepared the calculation of force-free motion on the unit sphere, following Hertz' take on mechanics. Since the constraints could be arbitrary and the principal would still apply, I wanted to set up the system in x,y,z rather than constraining motion to $r=1$ in a spherical coordinate system.

To do that we consider the movement of a point mass constrained to the unit sphere in $\mathbb{R}^3$. We let the point be a free mass located at $\boldsymbol{r}(x,y,z)=x(t)\mathbf{e}_x+y(t)\mathbf{e}_y+z(t)\mathbf{e}_z$ with the holonomic constraint $$g(x,y,z)=x^2+y^2+z^2-1.$$

We get then

\begin{align} \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\mathbf{r}}}\right) - \frac{\partial L}{\partial \mathbf{r}} &= \lambda(t)\nabla g(x,y,z) \\ m\ddot{\mathbf{r}} &= \lambda(t) \nabla g(x,y,z) \end{align}

which delivers 4 equations

\begin{align} m\ddot{x} -2\lambda x &=0 \\ m\ddot y -2 \lambda y &=0 \\ m\ddot z -2 \lambda z &=0 \\ x^2+y^2+z^2-1&=0. \end{align}

We multiply each equation by its coordinate and add together \begin{align} m\ddot{x}x+m\ddot yy+m\ddot zz &= 2\lambda (x^2+y^2+z^2) \\ \frac m2(\ddot{x}x+\ddot yy+\ddot zz ) &= \lambda. \end{align}

Using the second time derivative of $g$ we have $$\dot x^2+\dot y^2 +\dot z^2 = -(\ddot{x}x+\ddot yy+\ddot zz ) $$ we obtain $$\lambda = -\frac m2(\dot x^2+\dot y^2 +\dot z^2) = -\frac m2 \|\dot{\boldsymbol{r}}\|^2 $$ to get \begin{align} m\ddot{x} +m(\dot x^2+\dot y^2 +\dot z^2) x &=0 \\ m\ddot y +m(\dot x^2+\dot y^2 +\dot z^2) y &=0 \\ m\ddot z + m(\dot x^2+\dot y^2 +\dot z^2) z &=0 \\ \end{align}

or $$m\ddot{\mathbf{r}} +m\|\dot{\mathbf{r}}\|^2 \mathbf{r} = 0. $$

To demonstrate I integrated this first with a leapfrog integrator and found my point mass was not staying on the sphere, but was converging to a wrong result. After calling myself completely into question, I decided to try the Yoshida 4th-order integrator and got near-perfect results (constraints, conservation, etc.). I tried the problem in spherical coords and was also not conserving energy (although constraints satisfied).

Comparison of leapfrog (2nd-order symplectic) and Yoshida (4th-order symplectic) integration

What is so high-order about the problem that second-order integration won't work? How would one analyse the needed integration order?

Not a chance
  • 71

2 Answers2

2

You need to be careful in applying leapfrog to your EoM's since you have a velocity dependence on the force. You can have an appropriate second-order solver if you derive it using the same principles.

You can derive a Verlet analogue using the discretized least action principle: $$ S = h\sum_n \frac1{2h^2}(\vec r_{n+1}-\vec r_n)^2-F_n(r_n-1) $$ with $h$ the time step. You get the equations of motion: $$ \frac1{h^2}(\vec r_{n+1}+\vec r_{n-1}-2\vec r_n) = F_n\hat r_n $$ with $F_n$ chosen to normalise $r_n$. This gives you an implicit scheme: $$ F_n = \frac{||\vec r_{n+1}+\vec r_{n-1}||-2}{h^2}\\ \vec r_n=\frac{\vec r_{n+1}+\vec r_{n-1}}{|| \vec r_{n+1}+\vec r_{n-1}||} $$ which you can make explicit using the normalising constraints: $$ \vec r_{n+1}=-\vec r_{n-1}+2(\vec r_{n-1}\cdot\vec r_n)\vec r_n $$ In practice, due to finite precision issues, it is numerically unstable, and you should rather use: $$ \vec r_{n+1}=-\vec r_{n-1}+\lambda_n\vec r_n $$ with $\lambda_n$ chosen so that $\vec r_{n+1}$ is normalized without assuming that $\vec r_n,\vec r_{n-1}$ are. Without accounting for numerical error, the two approaches are formally equivalent, reserve the holonomic constraint and energy.

You can convert this Verlet analogue into leapfrog by inspection or by amending the least action principle. The new EoM's are: $$ \begin{align} \vec r_{n+1} &= \vec r_n +h\vec v_{n+1/2} & \vec v_{n+1/2} &= \vec v_{n-1/2}+hF_n\hat r_n \end{align} $$ with the same force as previously. Similarly, you can find it implicitly, explicitly numerically unstable or explicit numerically stable.

In short, there is no need for higher order solvers for your problem. You just need to be careful with how you implement your solver and watch out for numerical instabilities due to finite precision issues.

LPZ
  • 17,715
  • 1
  • 10
  • 36
0

To answer the titular question: there isn't such a rule. Effectively, it's up to you as the researcher to determine the best ODE scheme to use to solve the problem based on your wants.

For instance, if you are demanding high accuracy, you will want to use the highest order scheme available to you. On the other hand, if you are demanding speed you might be more interested in lower order schemes. For problems that require conserving energy, you will likely be restricted to symplectic methods. If you have a stiff system, then you'll have to use an implicit scheme.

Running your system through a bunch of schemes is pretty simple when you have a small system (in both number of variables & total time steps) as you can get a result to compare in a few seconds. When you have a larger system, it's a little more troublesome if the simulation takes hours/days.

See this Math.SE post or this one for other suggestions. There may be other suggestions on SciComp.SE, but I'm not sure.

Kyle Kanos
  • 29,127