Let's draw space-time diagrams. First from your perspective on Earth:
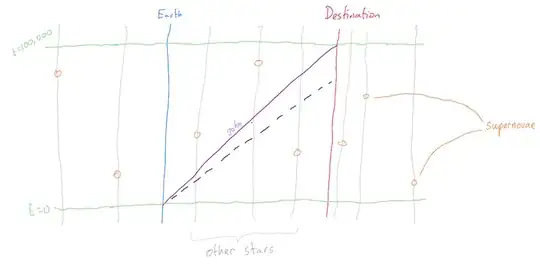
This is hopefully straightforward to read. At time $t=0$ (lower green line) John (purple line) leaves Earth and heads for the delta quadrant, at a speed slightly slower than light (black dashed line), arriving at time $t=100,000$ (upper green line). Meanwhile, supernovae (orange circles) occur at various other stars in the galaxy (grey lines).
Now let's draw the same diagram, Lorentz transformed into John's reference frame. (This is guesstimated but should be qualitatively correct.)

This probably looks a bit weirder at first. But we can work out what's happening. First, John's path is now vertical, since he is not moving from his perspective. All the stars are now moving past him, at close to the speed of light, so they have become diagonal lines close to 45 degrees. The light path (black dotted line) is still at 45 degrees, because the speed of light is constant in all reference frames.
What makes it look weird is that the green lines have also tilted. In relativity, simultaneity is observer-dependent: things that happen at the same time in one reference frame can happen at different times in another reference frame, and if events are space-like separated they do not even have to happen in the same order in both frames.
We can add in additional lines for $t=0$ and $t=500$ in John's reference frame:
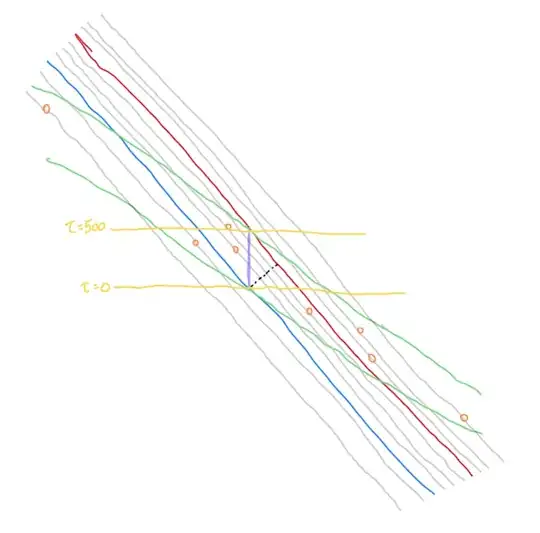
Now note that in the first diagram, there are 8 supernovae that occur between $t=0$ when John leaves Earth and $t=100,000$ when he arrives at his destination, while in the second there are only two supernovae that occur between $\tau=0$ when he leaves and $\tau=500$ when he arrives. So indeed, in John's reference frame there are fewer supernovae that occur during his journey than in yours.
But of course all 8 supernovae still occur in both diagrams. It's just that from John's perspective not all of them occur during his journey. Some of them occur before he leaves, and others occur after he arrives. This is the resolution to the paradox.
There are some subtleties about the above argument that can be appreciated with a bit of thought. The first is that, as several people have commented, John will not actually observe the supernovae until their light reaches him. To work out which supernovae he can observe, you can draw their future light cones and see if they intersect his world line. I leave this as an exercise to the reader. (If you do it on both diagrams you will find that my diagrams are not completely accurate. If they were, you would get the same answer for both diagrams.)
The second subtlety is that John's perspective will change when he accelerates and decelerates at the beginning and end of his journey. Although I didn't draw any, it is possible to have a supernova that occurs inside the yellow lines but outside the green ones. This means you can have a supernova that happens during John's journey in his reference frame, but when he comes to a stop, it will still be in the future. So from his perspective it happens twice! But he doesn't observe it twice, because its light will only reach him once, after he has arrived at the destination.