It is known that rigid bodies cannot exist in the framework of special relativity by causality arguments. But recently I saw a video on YouTube that claims rigid bodies are not compatible with Newtonian mechanics, namely the strong third law (PSE discussion here).$^\dagger$ The law basically states
For every force (action), there's a collinear reaction force of equal magnitude, pointing in the opposite direction.
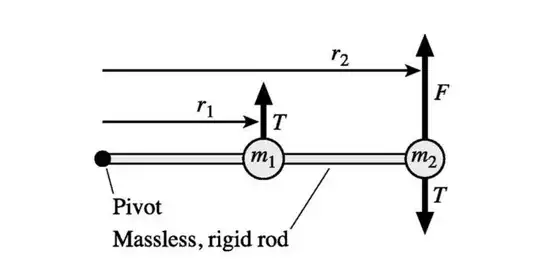
The video references this paper$^\ddagger$, which analyses the following two-body model and notes that the tangential force $F$ causing rotation contradicts the storng third law, assuming rigidity, since the reaction must not be collinear with action. Then the author goes through a calculation assuming non-rigidity, deriving the correct result, and concludes that
...rigid bodies are inconsistent with classical (non-relativistic) physics... The rigid-body model employed here violates the strong third law and angular momentum conservation (via Noether’s theorem), leading to a completely incorrect statement of the rotational second law.
However, opinions seem divided on the paper (i.e. this and the comments therein). My question is, is it true that the idea of rigid body is incompatible not just with relativity, but with Newtonian mechanics? If not, is there a problem with the formulation/application of the strong form of Newton's third law here?
$^\dagger$ I have left a comment under the video asking for clarification on the details of the "strong form", but my guess is that it is a statement about angular momentum conservation instead of linear momentum conservation.
$^\ddagger$ Cross, D. J. (2014). The physical origin of torque and of the rotational second law