Can torques cause both transitional and rotatory motion?

Question

Imagine a rod (a rigid body) 10 meters long that is freely floating in space without being attached at any point. Its mass is 12 kilograms and according to most sources I found, its moment of inertia can be calculated via the following formula:

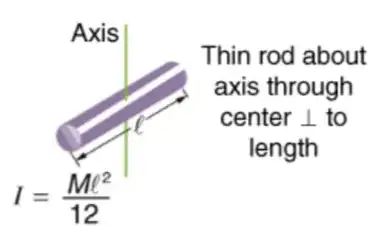
This makes its moment of inertia $100~\mathrm{kg}\,\mathrm{m}^2$.

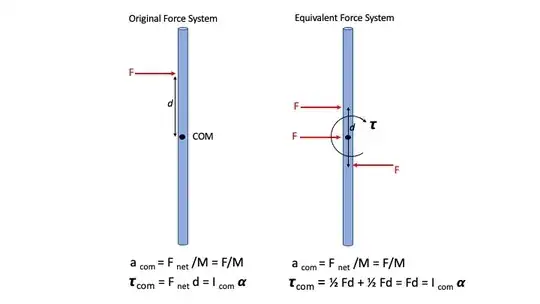
If a perpendicular force of 24 newtons was constantly applied to its center (the 5-meter mark), its translational acceleration would be $2~\mathrm{m}\,\mathrm{s}^{-2}$ and angular acceleration would be $0~\mathrm{rad}\,\mathrm{s}^{-2}$. Now, if the same force was applied a distance $0.1~\mathrm{m}$ to the right of the center, there would be a torque of $2.4~\mathrm{N}\,\mathrm{m}$, and hence an angular acceleration of $0.024~\text{rad}\,\mathrm{s}^{-2}$. Similarly, if the same force is applied at the end of the rod (at 5 meters away from the center) the torque is 120 Nm and the angular acceleration is $1.2~\text{rad}\,\mathrm{s}^{-2}$

From this we can see that as the force is being applied further from the center, the angular acceleration increases due to more torque.

I was wondering if the linear (transitional) acceleration gradually decreases as the force is shifted away from the center (case 1), or does it abruptly become 0 when the force shifts even slightly away from the EXACT center of the rod (case 2).

If case 1 is true, how do you calculate the transitional acceleration?

Answer 1

Question(s) #1: Would there be any linear (transitional) acceleration as a result of the force in the second scenario? If so, why? How do we calculate the magnitude of this transitional acceleration?

Yes to the first question. Linear and angular acceleration are independent properties.

To the second question, you apply Newton's 2nd law for linear acceleration, i.e.,

$$a=\frac{F_{net}}{m}$$

Question #2 (assuming answer to #1 is yes): Would there still be any transitional acceleration if the force is applied constantly to the end of the rod (resulting in a greater torque of 120 Nm and an angular acceleration of 1.2 rads^-2)? If so, would the magnitude of this acceleration be more or less compared to question #1. and why?

Yes there will still be translational acceleration, and it will be the same as if the force were applied perpendicular to any location along the rod. The reason it is the same is the translational acceleration and angular acceleration are independent.

For any point of application of the force along the rod, you can move the location of the application of the force, preserving its direction, to the center of mass as long as you include a force couple (torque) about the COM equal to the torque created by the force at its original location. The result is a force system equivalent to the original. See the figures below.

Question 3#: If the force and its duration is constant, then is the sum of its angular and transitional momentum constant?

No. Both would be constantly increasing. The angular and linear momentum is constant only after the force is removed. Momentum of a system (in this case the rod) is only constant in the absence of net external forces and torques.

Hope this helps.