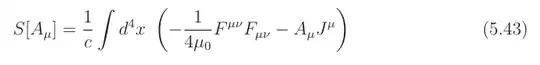Sign conventions for the Lagrangian from the EM Lagrangian density

Question

In Chapter 13.6 of the 3rd edition of Goldstein's Classical Mechanics, Goldstein proposes the Lagrangian density of the electromagnetic field as:

$$\mathcal{L} = -\frac{F_{\lambda \rho} F^{\lambda \rho}}{4} + j_\lambda A^\lambda.\tag{13.118}$$

He then goes on to pick a Lorentz frame to define a charge density:

$$\rho = q \delta\left ( \mathbf{r} - \mathbf{s} \right )\tag{13.122}$$

and current density

$$\mathbf{j} = q \delta\left ( \boldsymbol{\mathbf{r} - \boldsymbol{s}} \right )\mathbf{v}\left ( \mathbf{r} \right )\tag{13.123}$$

where $\mathbf{r}$ is the usual position vector, $\mathbf{s}$ is the position of the charge $q$, and $\mathbf{v}$ is the velocity of the charge. Then, he defines (not explicitly) the Lagrangian density as a sum the free-field term

$$\mathcal{L}_0 = -\frac{F_{\lambda \rho} F^{\lambda \rho}}{4}$$

and the interaction term

$$\mathcal{L}_\text{int} = j_\lambda A^\lambda$$

Then he says that the Lagrangian in this particular Lorentz frame is

$$L = \int dV \mathcal{L} = \int dV \mathcal{L}_0 - \int dV \rho \phi + \int dV \mathbf{A} \cdot \mathbf{j}.\tag{13.124}$$

My concern is with the signage of the last two terms involving the scalar and vector potential, $\phi$ and $\mathbf{A}$, respectively. Given that the four-potential is defined as

$$A^\mu = \left ( \frac{1}{c} \phi , \mathbf{A} \right )$$

and the (contravariant) four-current as

$$j^\mu = \left ( c \rho, \mathbf{j} \right )$$

using the metric signature that the book uses throughout, $\left ( +--- \right )$, then

$$j_\lambda A^\lambda = \rho \phi - \mathbf{A} \cdot \mathbf{j}$$

which has the opposite signage of the last two terms in $L$. Is this a mistake in the book, or am I missing something obvious? I'm thinking it's the latter due to the fact that

$$- \int dV \rho \phi + \int dV \mathbf{A} \cdot \mathbf{j} = -q \phi + q \mathbf{A} \cdot \mathbf{v}$$

which is the potential term of the Lagrangian for a charge $q$ in an electromagnetic field

$$L = \frac{1}{2} m \mathbf{v} \cdot \mathbf{v} - q \phi + q \mathbf{A} \cdot \mathbf{v}.$$

Answer 1

In Chapter 13.6 of the 3rd edition of Goldstein's Classical Mechanics, Goldstein proposes the Lagrangian density of the electromagnetic field as:

$$\mathcal{L} = -\frac{F_{\lambda \rho} F^{\lambda \rho}}{4} + j_\lambda A^\lambda$$

Although it is not listed in the official errata, I think the error is in the above-quoted equation (assuming the "mostly minus" metric is in use).

With the mostly minus convention, the Lagrangian density should be written as: $$\mathcal{L} = -\frac{F_{\lambda \rho} F^{\lambda \rho}}{4} - j_\lambda A^\lambda\tag{A}$$

See, for example, the development given here, which uses the mostly-minus sign convention, and which includes Eq. (5.43), as seen below, which is an expression consistent with Eq. (A) above.

Answer 2

Yes, OP is right:

1. Given that the Maxwell term is normalized as $-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}$ in the E&M Lagrangian density the source term should be $\pm j^{\mu}A_{\mu}$ if the Minkowski signature is $(\mp,\pm,\pm,\pm)$, respectively, cf. e.g. my Phys.SE answer here.

2. Apparently Goldstein forgot to change the sign in front of the source term when he changed the Minkowski signature from $(-,+,+,+)$ [or with an imaginary time] in the 2nd edition to $(+,-,-,-)$ in the 3rd edition.

Answer 3

The signage is already set by prevailing conventions. You can tell by looking at the expression for the electric field in terms of the potentials: $$ = -∇φ - \frac{∂}{∂t}$$ and comparing it with the tensor expression $F_{μν} = ∂_μ A_ν - ∂_ν A_μ$. If, in a frame with Cartesian spatial coordinates, you adopt the convention $\left(x^1, x^2, x^3\right) = (x, y, z)$, with $x^0 = t$, then you have $\left(∂_1, ∂_2, ∂_3\right) = ∇$ and $∂_0 = ∂/∂t$. So, if you set the spatial components of the potential as $ = \left(A_1, A_2, A_3\right)$, then in order to get compatibility between the expression for $$ and for the mixed space-time components of $F_{μν}$, that forces your hand and you have to adopt the opposite sign $A_0 = -φ$ for the scalar potential and set the mixed components of $F_{μν}$ as $ = \left(F_{10}, F_{20}, F_{30}\right)$.

For the magnetic field, compatibility with the relation $ = ∇×$ requires that you set $ = \left(F_{23}, F_{31}, F_{12}\right)$.

Under the Maxwell-Lorentz Lagrangian density $_0 = -¼ Y_0 \sqrt{|g|} g^{μρ} g^{νσ} F_{μν} F_{ρσ}$, you can actually scale the metric by any non-zero constant factor which means you can adopt any authors' conventions what signs to adopt for the metric components, since this expression is invariant with respect to constant non-zero re-scaling of the metric. Different conventions are in force to handle the coefficient $Y_0$, but the omission of $\sqrt{|g|}$ (which a lot of authors are guilty of) is careless, since non-Cartesian coordinates need it - even in flat space-time. That's why I put the initial emphasis on "with Cartesian coordinates".

In terms of the components just laid out, for a Minkowski metric (i.e. one where $g_{μν} = 0$ if $μ ≠ ν$, where $g_{11} = g_{22} = g_{33} = -g_{00}/c^2$ and $g_{00} ≠ 0$), you'll get the expression $_0 = ½ Y_0 \left(E^2/c - B^2 c\right)$.

The Euler-Lagrange equations make use of the derivatives with respect to the Lagrangian density. To get things to work consistently and to yield the inhomogeneous Maxwell equations $$∇· = ρ,\quad ∇× - \frac{∂}{∂t} = ,$$ you'll have to set the derivatives, up to a constant factor, as $$ = +\frac{∂}{∂},\quad = -\frac{∂}{∂},\quad ρ = -\frac{∂}{∂φ},\quad = +\frac{∂}{∂}.$$

All the dependence of $$ on $(,)$ is locked up on $_0$, whose expression has already been laid out, with the result being: $$ = \frac{Y_0}{c} = ε_0 ,\quad = Y_0 c = \frac{}{μ_0},$$ in SI, so that $ε_0 μ_0 = 1/c^2$ and $Y_0 = ε_0 c = 1/(μ_0 c) = \sqrt{ε_0/μ_0}$. That's the free space admittance and $Y_0$ is the actual symbol used for it. So, the Maxwell-Lorentz Lagrangian density is actually just $$_0 = \frac{ε_0 ||^2}2 - \frac{||^2}{2 μ_0}.$$

Finally, if the part of $$ that depends on the potentials $(φ,)$, is linear in the potentials, then the above differential relations for $$ force your hand and you'll have to write it as $· - ρφ$, giving you a total Lagrangian density of: $$ = \frac{ε_0 ||^2}2 - \frac{||^2}{2 μ_0} + · - ρφ.$$

In component form, the derivatives are actually tensor densities, rather than tensors and one would express them as $$ = \left(^{01}, ^{02}, ^{03}\right),\quad = \left(^{23}, ^{31}, ^{12}\right),\quad ρ = ^0,\quad = \left(^1, ^2, ^3\right), $$ with $^{μν} = Y_0 \sqrt{|g|} g^{μρ} g^{νσ} F_{ρσ}$ and $· - ρφ = ^μ A_μ$. Another way you can tell that the components of the current 4-vector are actually components of a tensor density, for your case, is that the expression has a delta function in it and the delta function is actually a density here, simply by virtue of the way it appears in integrals. In component form, you'd get $^μ(,t) = e (ds^μ/dt) δ( - (t))$.

This tends to be obscured by two things: (1) a lot of authors mix $c$'s into all of this. None of that should be there, the only dependence on metric or space-time structure is encapsulated in the relations $ = ε_0 $ and $ = μ_0 $, which you can see by the equation, just cited, between $$ and $F$. There's no involvement of metrics or $c$'s anywhere else ... unless one uses different conventions that inject $c$ into the picture. In particular, you can use the other Maxwell equations even in non-relativistic electromagnetic theory as is. They mostly match the forms that Maxwell, himself, used, apart from a scale change in $$ by $4π$.

That brings us to: (2) the theoretical literature still uses Gaussian units or other similar "normalized" systems, which is guilty of (1). Most other places are now on the same page as the ISQ standard (or SI), which is free of the problem in (1). For the Lagrangian density, that entails adding in $Y_0$. Here, I simplified the description of the account of the conversion between the two conventions. The $Y_0$ coefficient would drop out in Gaussian, which is what "Different conventions are in force to handle the coefficient $Y_0$", above, is alluding to.