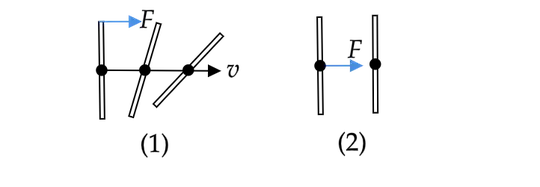1

If I have a stick with even mass distribution, and for scenario (1) I give it an instantaneous force at the tip, how can I determine the speed of the center of mass? Is it by Newton's second law? Also how do I determine the angular velocity about the center of mass? Do I see the force as a torque now? Does it play two parts in this case?

Then for scenario (2), I should have the same linear speed right? Since they both have the same net force.

But where did the extra angular moment in scenario (1) come from? I don't understand, I have done the same amount of work in these two cases right? Any help would be appreciated!

enter image description here

Qmechanic
  • 220,844
min
  • 13

1 Answers1

2

You probably mean that you applied a short-duration force in both cases of your drawing with the same [impulse], so let's say the same force $F$ for the same short time $\Delta t$. Everything you write in your analysis is then correct except the assumption at the end that you have done the same amount of work.

That's because the amount of work depends on how much the rod will move in this short time $\Delta t$. In situation (2) it will move less. You can see that easier if you change the mass distribution a little bit, into this:

two masses

When pushing at one end, you are in that case just accelerating one mass while the other remains almost stationary. When pushed in the middle, the two masses are felt as one twice as heavy mass and the point where you touch the rod will move only half as far in time $\Delta t$, so you do half the amount of work, consistent with the fact that in that case you do not have to provide the rotational energy.

Jos Bergervoet
  • 6,031