It is my understanding that just as special relativity contracts length with velocity general relativity contracts length with gravity. Would this mean the radius of a BH is smaller than it would appear without the gravitational effects?
2 Answers
In this answer, I am ignoring optical effects and illusions of how a body would appear to look from a distance and focussing on actual measurements of length.
Starting with the Schwarzschild metric, and using the $(-,+,+,+)$ signature convention, we can set $\mathrm{d}t=0$ and $\mathrm{d}\Omega = 0$ and obtain $$\mathrm{d}s = \frac{\mathrm{d} r}{\sqrt{1-2M/r}}$$ using units such that $c=1$ ang $G=1$. This is the gravitational length contraction factor and is measured vertically. $\mathrm{d}r$ can be thought of as the proper length of an infinitesimal ruler measured locally and $\mathrm{d}S$ as the coordinate length of the ruler measured by an observer at 'infinity'. To calculate the vertical ruler length between two radial coordinates, we simply have to calculate the definite integral of the above equation using suitable radial coordinates for the limits. When we do this, we find the ruler distance between two radial coordinates that are one unit apart is greater the nearer we get to the event horizon because the rulers are length contracting, and it requires more of the rulers to span the distance between the radial coordinates.
Just for info, the proper ruler distance is approximately the average of the radar distance measured from the upper coordinate and the radar distance measured from the lower coordinate.
Surprisingly, we can use the event horizon as the lower limit, but if we try to use a lower altitude than $2m$ as the lower limit, we start getting complex results, representing the fact we cannot have stationary observers or stationary rulers below the event horizon, making it difficult to calculate the proper ruler distance from somewhere inside the event horizon, to somewhere outside the event horizon.
I came up with a way we can get an idea of what the proper ruler length measured from the centre is.
We start with the interior Schwarzschild solution, which is the metric for a fluid body that has a physical surface. (A small, low-density object could float on this surface.) For $r>2m$ (before the black hole has formed), it is still possible to have stationary rulers and observers all the way to the centre, so a physical proper ruler distance can be defined.
Setting $\mathrm{d}t=0$ and $\mathrm{d}\Omega = 0$, we obtain $$\mathrm{d}S = \frac{\mathrm{d}r}{\sqrt{1 - 2M r^2/R^3}},$$
where $R$ is the radius of the fluid body. When integrated with respect to $r$, we get the distance from the centre ($r=0$) to the surface ($r=R$) as:
$$ S(r) = \int\limits_0^{R}{\frac{\mathrm{d}r}{\sqrt{1 - 2M r^2/R^3}}} = \sqrt{\frac{R^3}{2M}} \sin^{-1}\left(\sqrt{\frac{2Mr^2}{R^3}}\right).$$
Setting $r=R$ and $M=1$, we can define the distance $S$ as a function of $R$ as:
$$ S(R) = \sqrt{\frac{R^3}{2}} \sin^{-1}\left(\sqrt{\frac{2}{R}}\right)$$
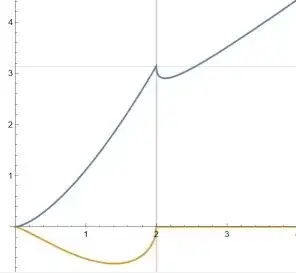
and the plot of the function gives:
where the orange curve represents the imaginary part of the distance. If we set the coordinate $R$ arbitrarily close to $2M$, then the proper radius becomes arbitrarily close to $\pi M$. The Newtonian expectation for the circumference of an object with radius $R = \pi M$ is $2 \pi R = 2M \pi^2$, but the Schwarzschild circumference is $4M \pi $, which is smaller. In this way, we can consider the coordinate radius of the object to be length contracted. For $R<2M$, the result has a mon zero imaginary part. We cannot get a sensible answer for $R<2M$ because the interior metric is a static solution, and for $R<2M$, the radius is not static. More technically, the result is only valid for $R<18M/8$ because the force at the centre becomes infinite at that radius, and the object has to collapse, but nevertheless, this analysis gives an idea of how the proper and coordinate radii differ. A more exact analysis could probably be done on a Tolman dust model where internal pressure does not complicate the issue.
In summary, in Schwarzschild metric, restricting ourselves to bodies with radii greater than $2M$, proper vertical coordinate lengths are shorter than their proper lengths, similar to how in SR, proper lengths parallel to the motion are shorter than their proper lengths.
It is rather inaccurate to say that gravity contracts length in the same way as special relativity. Gravity is the curvature of spacetime as a whole which is a different concept from special relativistic length contraction, which occurs on flat spacetime. The time dimension is also involved. Due to spacetime curvature, the apparent "disk", or shadow, of a Schwarzschild black hole actually spans a radius of $3\sqrt{3}r_s/2 \approx 2.6r_s$ where $r_s$ is the Schwarzschild radius. This is demonstrated in this post and this animation. This phenomenon is known as gravitational lensing.
Even for highly dense objects such as neutron stars, gravitational lensing enables more than one hemisphere to be seen at the same time. So spacetime curvature causes it to appear larger rather than smaller.
- 15,416