Can we treat the entire mass of the spheroid as being concentrated at its center?

Question

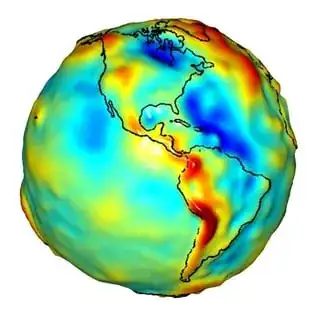
I know that to find the gravitational force between two objects, if either of them is a sphere, we can assume its mass to be concentrated at its center and use the formula for gravitational forces for point masses. However, in my textbook (Cengage Physics, Mechanics - II), to find the gravitational force exerted by the Earth on masses at the equator and poles (where they showed the Earth as a spheroid), they used $\frac{GM_E m}{R_{eq}^2}$ and $\frac{GM_E m}{R_{pole}^2}$ respectively. But I think that is wrong because the Earth, being treated as a spheroid in this case, cannot exhibit the behavior that spherically symmetric masses do.

Answer 1

You are correct. Gravity around a spheroid is not the same as gravity around a sphere. The J2 perturbation accounts for the Earth's ellipsoidal shape, and technically one has to account for it. However, it is reasonably small so can often be ignored. Satellite operators, however, do need to account for this effect. Indeed, when you really look at it, the Earth's gravitational field is anything but simple