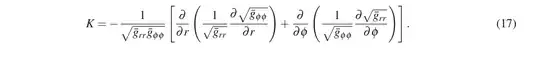I am trying to calculate Gaussian curvature of an optical metric
$$ d \sigma^2=\frac{r\left(\omega_{\infty}^2-\omega_e^2\right)+2 m \omega_e^2}{(r-2 m) \omega_{\infty}^2}\left(\frac{d r^2}{1-\frac{2 m}{r}}+r^2 d \varphi^2\right) $$
The paper gives the results as ->
$\mathcal{K}=\frac{\omega_{\infty}^2 m}{r^3\left(\omega_{\infty}^2 r-\omega_e^2 r+2 \omega_e^2 m\right)^3} \times\left[\left(3 \omega_e^2 \omega_{\infty}^2-2 \omega_{\infty}^4-\omega_e^4\right) r^3+\left(-9 \omega_{\infty}^2 \omega_e^2+3 \omega_{\infty}^4+6 \omega_e^4\right) r^2 m+\left(6 \omega_{\infty}^2 \omega_e^2-12 \omega_e^4\right) r m^2+8 \omega_e^4 m^3\right]$
Now they approximating this by taking only first order of m which reads $\mathcal{K} =-\frac{(2 \omega_{\infty}^2-\omega_e^2) \omega_{\infty}^2}{r^3\left(\omega_{\infty}^2-\omega_e^2\right)^2} m +\mathcal{O}\left(m^2\right)$.
How they are doing this? Especially how they’re taking approximation & coming to final results. I’m trying to calculate by using the following formula
But the results is too vast to calculate. How should I progress and get Gaussian curvature for metric for calculating bending angle?