0

I wanted to check my understanding of special relativity and set up one experiment that could lead to deriving the Lorentz factor. Usually, the deriviation for the Lorentz factor is explained using a light clock forming a 90° angle with the direction in which the observer is moving.

1

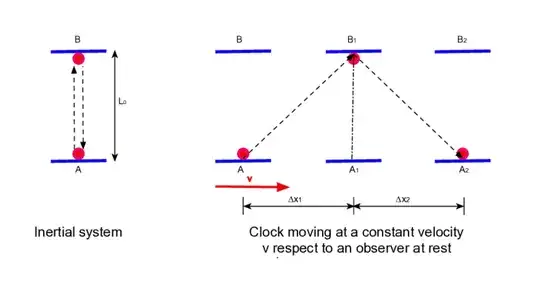
Here, we see that the direction in which the light ray is moving, is perpendicular to the moving direction. And if you calculate the time it takes for the light in both of the light clocks(in each reference frame), the relationship between the two turns out to be exactly $1/\sqrt{(1-v^2/c^2)}$, which is the right Lorentz factor.

However, you could follow a similar logic and consider the case in which the light clock is leaning on its side and shooting light rays in the direction of motion.

2

Let's suppose that a moving observer is moving from left to right horizontally. He or she holds a light clock that lay horizontally with the direction of motion. The distance of the light clock is a and the observer is moving at the speed $v$ relative to the stationary observer. The stationary observer can measure his or her time with the identical light clock. Time on each reference frame is defined as the time it takes for the light to bounce back to the observer, so we would be able to say that we can find the relationship of the time of the stationary observer and the time of the moving observer which is the Lorentz factor. I wonder why my result $c/(c^2-v^2)$ does not match the real Lorentz factor. Were my assumptions wrong? Why does it work when the light clock is perpendicular to the moving direction, but doesn't when it is facing the direction of motion?

Vincent Thacker
  • 15,416
Chanseo
  • 11

1 Answers1

2

Your calculations assume that the observers agree on the length of Alice's clock.

For the vertical clock, that's the right assumption. Here is why: Alice can put little dabs of paint on the top and bottom of her light clock, which brushes against Bob's identical light clock as it passes, leaving marks. If according to Bob, her light clock is shorter or longer than his, he'll be able to verify that by the locations of the marks --- and she'll have to agree because the marks are there for all to see. Then they'll agree on whose clock is shorter, and can use this to reach agreement on who's moving, contrary to the first principle of relativity: There's no objective way to determine which inertial observer is in motion.

No analogous experiment forces Alice and Bob to agree on the length of a horizontal light clock, so they don't have to agree. And in fact your calculations shows that they can't agree on the length of the horizontal clock, because if they did, they'd caclulate the wrong value for time dilation.

WillO
  • 18,387