Suppose we have two plates which have unequal magnitudes of charge. When we connect these plates to a battery, why does the charge on both plates become equal and opposite? Why is capacitance defined for equal magnitudes of charge?
2 Answers
Suppose we have two plates which have unequal magnitudes of charge.
In order for the two plates of a parallel plate capacitor to have significant unequal magnitudes of charge, it would have been necessary to charge them separately by some external means before bringing them together to form a capacitor. An initially neutral capacitor charged by a battery will not have any significant imbalance of charge. (See @John Doty answer).
When we connect these plates to a battery, why does the charge on both plates become equal and opposite?
The charge on the inner surfaces of the plates facing each other doesn't become equal and opposite due to connection to the battery. They are already equal and opposite before connecting them to the battery, as follows:
When one plate with charge $Q_1$ and another plate with charge $Q_{2}\lt Q_1$ are brought together to form a capacitor the charges will distribute in such a way that on the inner sides of the capacitors facing each other there will be equal and unlike charges $q$ and $-q$, according to
$$q=CV\tag{1}$$
where $C$ is the internal capacitance (see @John Doty answer) defined by eq (4) and $V$ is the difference of potential due to the uneven distribution of charges. For conservation of charge, the outer sides will have charges $Q_{1}-q$ and $Q_{2}+q$, of equal magnitude and sign. Since these outer charges are at the same potential they do not contribute to the potential difference $V$ across the plates.
It can be shown, as described in the link below, that the magnitude of the equal and unlike charge $q$ is given by
$$q=\frac{1}{2}(Q_{1}-Q_{2})\tag{2}$$
And that the outer sides we will have charge of the same magnitude and sign,
$$Q_{1}-q=Q_{2}+q=\frac{1}{2}(Q_{1}+Q_{2})\tag{3}$$
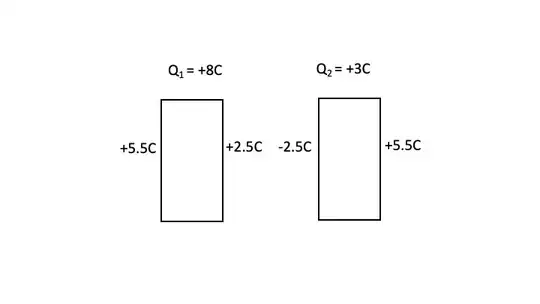
EXAMPLE (See FIG below):
A plate with charge $Q_{2}=+3C$ and another with charge $Q_{1}=+8C$ are brought together to form a capacitor. Per equation (2) the charge will distribute with $q=2.5C$ on the inside surface of plate 1 and $q=-2.5C$ on the inside surface plate 2. Per equation (3) the charge on the outside surface of both plates is +5.5C
If this capacitor is then connected to a battery having the same voltage $V$ as the charged capacitor, nothing should change.
Why is capacitance defined for equal magnitudes of charge?
The internal capacitance is not “defined” for equal magnitudes of charge. Capacitance is a geometric property. For a parallel plate capacitor (ignoring fringe effects), its internal capacitance is defined by the equation
$$C=\frac{A\epsilon}{d}\tag{4}$$
So the internal capacitance is the same for equal or unequal magnitudes of charges on the plates.
Hope this helps.
- 81,786
Textbook capacitors have equal and opposite charge on their plates. Real capacitors don't: they have an internal capacitance and an external capacitance.
The external capacitance represents the ability of the capacitor to store a charge that isn't balanced between the plates. If you like, it's the capacitance between the capacitor as a whole and the rest of the universe. It's generally small, so it takes a large potential to create a small charge imbalance. Thus, you can often ignore it in practice.
The capacitance of textbooks and capacitor labels is the internal capacitance.
A battery has an external capacitance, too, so when your capacitor is connected to the battery it shares its external charge with that.
- 22,119