Rotational mechanics in collision of a mass and a rod

Question

Suppose a small particle of mass $m$ moving at a velocity $v$ collides with a rod at the end in a perpendicular direction to the rod. I am sure that the rod translated in the direction same as the direction of velocity of particle (by linear momentum conservation), but for the rotation of the rod, I'm not quite sure why it does always rotate about center of mass, can it rotate about any other point? Or can it rotate about every point on the rod depending on the frame we choose on rod?

Answer 1

In general, if you pick any point $p$ of a rigid body, the instantaneous motion of the body can be decomposed into the sum of the translational motion of $p$ and rotation about an axis passing through $p$. So, in this sense, the object can be considered to be instantaneously "rotating" about any of its points. But only instantaneously, because the velocity of $p$ at subsequent times need not remain the same as the inertial frame comoving with $p$ at that instant.

However, in this case, after the collision, there is no net force acting on the rod. Its center of mass will move inertially with constant velocity. No other point does. So its motion as a whole is translation of the center of mass and rotation about the center of mass. Using the center of mass and an inertial frame simplifies calculations significantly.

See this post for more information.

Answer 2

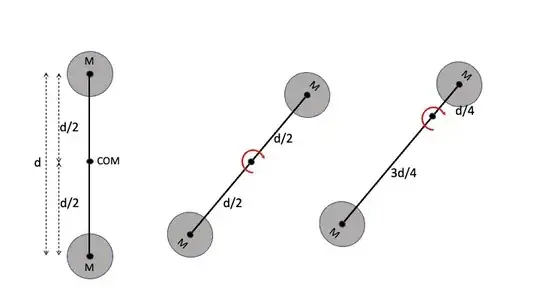
Assume no gravity and a uniform rod.

After the impact there are no external forces acting on the rod. That means the center of mass (COM) must move at constant speed in a straight line, per Newton's first law. In order for this to occur, given the rod rotates due to the impact not being on the COM, the center of rotation (COR) of the rod must be the COM. If it were not, you would have an imbalance of the centripetal forces acting on the masses on each side of the COR, giving the COM an acceleration along the axis of the rod.

See the figure below. To simplify things replace the rod with two equal spherical masses on each end. The middle figure shows the COR being the COM. The right figure shows the COR at other than the COM. The centripetal force acting on each mass is given by

$$F=mr\omega^2$$

Where $r$ is the distance of each mass to the COR and $\omega$ is the angular velocity of each mass about the COR, which is the same for each mass. For the COR located at the COM, the centripetal force acting on each mass is the same. But for the COR not at the COM the centripetal force is greater for the mass located furthest from the COR. That gives a net force acting along the rod, which would only be possible if there was a net external force acting on the rod.

Hope this helps.

Answer 3

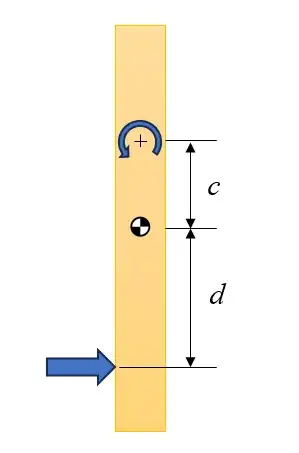
After the collision, if the center of mass has any velocity then indeed the center of rotation is not at the center of mass by definition.

Geometrically the center of rotation is at the pole of the polar line defined by the impulse. Actually, the center of rotation is always on the other side of the center of mass, so the COR location is in the reflection of the pole.

_{See pole-polar relationship for the concept.}

For any rigid body, given a force or impulse acting a distance $d$ from the center of mass, the instantaneous center of rotation is located a distance 4c$ away from the center of mass given the formula

$$ c = \frac{I}{m d} =\frac {\kappa^2} {d} $$

where $I = m \kappa^2$ is the mass moment of inertia about the rotation axis, and $\kappa$ the radius of gyration of the body.

As you can see, if the impulse acts on the center of mass with $d \rightarrow 0$ then the center of rotation goes to infinity $c \rightarrow \infty$ which corresponds to a pure translation.

The opposite is true, that to rotate a body about the center of mass with $c=0$, the offset distance of an impulse must be at infinity. This only happens in real life when there is a force-couple, or am impulse couple of two equal and opposite impulses acting.