The electron and proton have opposite charges, yet they somehow don't get attracted to each other and stay stable. By attraction, here I mean colliding into one another like magnets with opposite poles do. Why is that?
2 Answers
As far as I know, this was the question sparking quantum physics. Because, as you intuitively visualise, they should collide eventually. Since there is no such thing as a perpetuum mobile.
However, belief in particles adhering a principle of remaining in quantised states (often visualised as orbits, although frequencies and energy-levels seem to be more appropriate) was considered to 'solve' this problem.
Energy is then required to change the state of an electron. But a state is assumed to be sustained forever (disregarding proton decay over billions of years), unless internal energy is affected by something external to the atom.
This principle does not come with a theoretical basis for why particles have this 'want' to occupy- and remain in certain states. Or why those states are sustainable without spending energy.
The reason that in ordinary nature, that the proton and electron do not "combine" even though there is an attraction, is electronic attraction is not the only contributor to the overall attraction.
According to quantum mechanics, the Schrodinger Equation can be applied to determine not just the electric attraction, but also other "attraction" or "repulsion" contributions, with the Hydrogen atom as the simplest to understand the concept.
The electron is not just a point particle that can "fall" into the nucleus. It is spread-out, because confinement increases the kinetic energy necessary to keep the electron confined, in effect a "repulsion". When the spread of the electron and the attraction of the nucleus are equal and opposed, the the Schrodinger Equation provides the wave function that describes this spread for the election, with the proton very highly confined in contrast opposite in its electrostatic attraction. In the region very close to the nucleus (the proton), there is only a very small probability of the election approaching there, an insufficient amount for the combination reaction in ordinary nature.
From the Stack Exchange Physics Article, "Does the electron capture process ever occur in hydrogen?" (where electron capture would be the combination in the case of Hydrogen of its electron and proton), there is the following answer:
A free neutron has more energy than a proton and electron. The decay reaction is spontaneous and releases a neutrino as well.
The reverse reaction would require energy input. That energy is not available in any bound $^1$ atom.
This article, "Electron Capture" has more detail as to the process. In its reference to electron capture from Carbon to form Boron (an element one-left on the periodic table), when an atom captures an electron, one of its protons is converted to a neutron, and a Neutrino is ejected. The difficulty is that if ever enough energy is given to focus the electron sufficiently on the lone proton in Hydrogen to start such a reaction, a lone neutron is unstable and very quickly decays, also releasing a neutrino. Such lone neutron under ordinary circumstances is thus not generally observable.
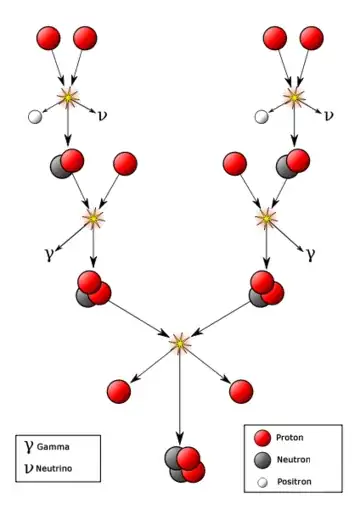
From the diagram in the article "Nuclear Fusion Inside the Sun", it shows various atomic-level reactions, including at top-right the reaction of two lone-protons inside of the core of the sun to form a positron, a neutrino, and a combination of a neutron and positron. Even in the extreme conditions of the core of the sun, lone neutrons are not stable enough to be found in the standard fusion reactions creating Helium from two lone Hydrogen protons.
As the electron is restricted in nature to insufficient energy to confine it with the proton sufficient for the overall reaction of the proton and electron combining to become a free neutron, in ordinary nature this reaction does not occur frequently enough to be observed, except in scientific experiments that are able to increase the kinetic energy of the electron sufficiently for it to be combined and bind. And then, of course, because of the associated instability, even in the case that the electron is driven to sufficiently high energy not ordinarily found in nature, to observe the immediate decomposition atomic reaction with its associated neutrino release is much easier than to observe the very short-lived unstable lone neutron itself.
- 300