Ring Magnet with a wire in the middle

Question

I have a very specific question concerning a system with a magnet and a wire.

Consider a ring magnet with a magnetic field directed right through its center. In the center of the magnet is a wire, through which a current $I$ is flowing. This also creates a magnetic field around the wire.

Correct me if I am wrong but I think the resulting force on the wire should push it right into the middle of the magnet.

The remaining question that I have is how do I calculate resulting force in this contraption, which is dependent on the magnetic field $B$ of the magnet on its inside and the current flowing through the wire?

I have put a sketch right below for you to understand it better.

Answer 1

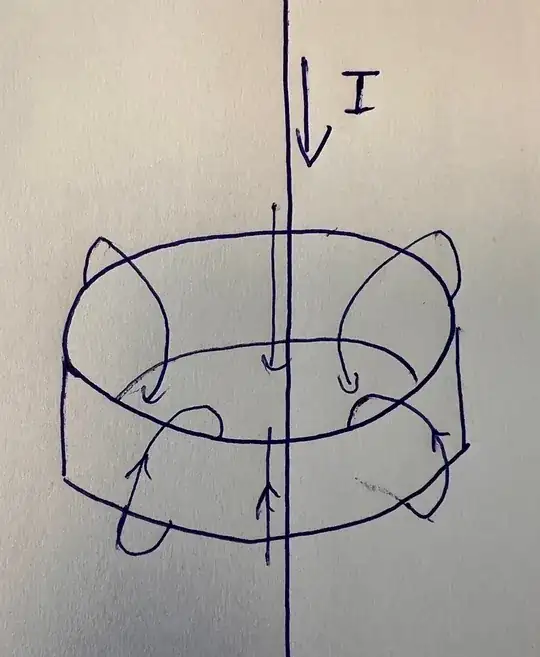
In magnetostatics, permanent magnets and electromagnets have the same effect, so for the computations, I'll assimilate the ring magnet as a solenoid. There are many methods for computing the force. The short answer is that paradoxically, the magnet applies no net force on the wire. Naturally, this will not apply anymore for AC currents, and only holds for DC currents. It's still a good sanity check for the AC case, as it means that the force is proportional to the frequency hence the canceling at zero frequency.

The first natural method is to integrate the force applied by the solenoid's field on the wire: $$ F = I\int B\times ds $$ with $B$ the field generated by the solenoid and $ds$ the line element of the wire. You would therefore first need to compute the field $B$ which does not have a simple expression and then integrate it making it complicated.

Another way is to first compute the mutual inductance of the wire and the solenoid $M$. It describes the interaction magnetic energy between the two that will depend on the position of the wire. More precisely, at fixed currents, $-M$ describes the mechanical potential energy between the two currents due to the magnetic force's work. The wire, if free to move, will therefore try to maximise $M$ and a maximum in configuration would correspond to a stable mechanical equilibrium.

Computing the mutual inductance is much easier, you just need to compute the flux of the field of one of the currents across the other current. The solenoid generates a field in the $r,z$ plane, so the flux across the wire is zero as can be seen by taking a half plane that contains the solenoid's field. Equivalently, the flux of the wire's field across any current loop forming the solenoid is zero, since the field is orthoradial and you can take a surface to be the disk perpendicular to the axis.

To conclude, the mutual inductance is zero, no matter the position of the wire. By taking the derivative, the force is zero, so the equilibrium is neutral.

Note that if you allow the wire to rotate, part of the reasoning is salvageable. Mutual inductance is zero as long as the wire lies in a plane of symmetry of the solenoid. When it leaves it, you have a non zero mutual inductance. In fact, you can prove that the wire being parallel to the axis of the solenoid is an unstable equilibrium. The wire will tend to align with the direction of the current of the solenoid's loop (i.e. tilt) and is repelled from the center.

Hope this helps.

Answer 2

Both magnetic fields are highly inhomogeneous.

Using this online simulator here we get the following results of the generated magnetic vectors:

$1)$ Current line $10A$. Current is flowing out of your monitor screen perpendicular, and towards you.

Fig.1 Current line Magnetic Vector Field simulation

Simulation Link: https://www.falstad.com/vector3dm/vector3dm.html?f=InverseRotational&d=vectors&sl=none&st=20&vd=16&rx=0&ry=0&rz=0&zm=1.2

Note: You can hold the simulation image and rotate it.

$2)$ Current loop (i.e. this is analogue for a single loop with the field of a ring magnet), North magnetic pole of field is facing you, current in the loop is moving counterclockwise.

Fig.2 Ring magnet Vector Field simulation

Simulation Link: https://www.falstad.com/vector3dm/vector3dm.html?f=CurrentLoopField&d=vectors&sl=none&st=20&vd=16&a1=40&rx=73&ry=0&rz=0&zm=1.2

Note: You can hold the simulation image and rotate it.

Assuming the ring magnet is mechanically fixed in place and cannot move and the wire line can move from the center position and using vectors superposition it is clear that the current wire cannot remain balanced at the center and will be attracted by the ring magnet's inner walls.

Furthermore, Earnshaw's theorem states that it is impossible to balance two inhomogeneous static magnetic fields.

Fun factor: Assuming you are not using a d.c. current on the wire line but an a.c. current instead of very low frequency, say 2-5 Hz then I predict the wire will rapidly move and collide with the inner walls of the ring magnet at different random positions each time resembling the rapid mechanical switching of an electric relay device.

Answer 3

The force on a charge $q$ with velocity $\vec v$, in a magnetic field $\vec B$, is $\vec F=q\vec v\times\vec B$.

Using cylindrical coordinates, wire initially in $z$ direction at $r=0$, so the velocity of the charge is in the $z$ direction. Magnet centered at $z=r=0$, so at $r=0$, its magnetic field is only in $z$ direction, so no force on wire since the velocity is parallel to the field and the cross product is zero, $q\vec v\times\vec B=0$.

Now make an infinitesimal displacement of the wire outward in the $r$ direction at $\theta=0$. The velocity of the charge is still in the $z$ direction, but the magnetic field now gets an infinitesimal $r$ component, not a $\theta$ component, and then the cross product $q\vec v\times \vec B$ gives an infinitesimal force in the $\theta$ direction, so it seems to me, at first glance, to be neither a restoring force back to center in the $r$ direction, nor a force to pull the wire to the inside edge of the ring magnet along the $r$ direction, rather a force to deflect circularly in the $\theta$ direction.

At 2nd glance I'd add that at $z=0$ there's no force still as the $\vec B$ field only has a $z$ component. The infinitesimal $\theta$ force occurs above $z=0$, and below $z=0$ the $\theta$ force occurs in the opposite direction.