Why would two different sized bikes not arrive at the same time starting from rest on the same slope?

Question

I was cycling with my little sister who was a little upset by the fact that I would arrive first at the end of a small bridge when we both started from the middle (where the plane is not inclined). Once we arrived home our dad told her that there was nothing to complain about as I am heavier than her.

I am pretty sure my dad is incorrect as g, the gravitational acceleration is the same for my sister and I, however I can't figure out the right answer.

Let's say hypothetically that we were next to each other, at rest, and began descending at the same time for a straight inclined plane. Now could the size of the wheels actually make me get down faster? I guess that having smaller wheels means that it would require many more revolutions to travel the same distance.

Just to clarify the bikes are simply rolling. Because of the different size of the bikes it is likely that the gear ratio may be different.

I am aware that there are many different variables to consider. For example the pressure of the tyres: which should be supposed to be sufficient to make the tyres decently filled with air.

Answer 1

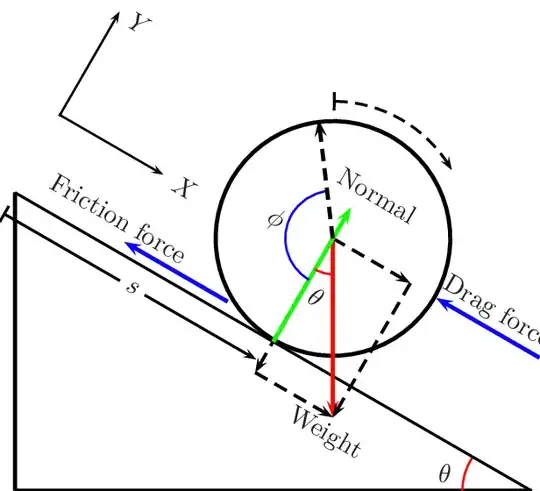
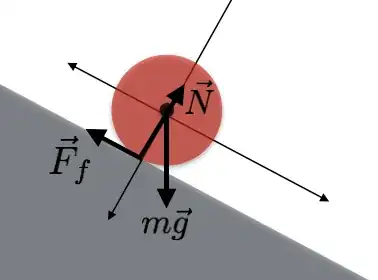
The main force slowing down a fast moving bicycle is air drag.

When you're rolling down a slope, gravity is speeding up your bike while drag is slowing it down. The force of gravity is proportional to your mass (plus that of your bicycle) while the drag force is proportional to your frontal area and approximately proportional to the square of your speed relative to the air.

Yes, there's also some friction in the wheel bearings and some rolling drag between the wheels and the ground. Like gravity, rolling drag is typically also proportional to weight, so if it was the only thing slowing your bike down, you would indeed expect the weight of the rider not to matter.

However, at speeds above about 20 km/h or so air drag will exceed rolling drag, and even at lower speeds (unless you're going very slowly or driving in deep mud or snow, or unless your bike is super rusty and never oiled) the effect of air drag is still noticeable. (That's also why it's so much harder to drive a bicycle against the wind than with the wind behind you.)

Thus there is still a significant component to the total drag force that's not proportional to your mass but to your frontal area.

For two objects of similar shape and composition, such as two humans, mass is approximately proportional to volume, and thus to height cubed, while frontal area is only proportional to height squared. Thus, the ratio of gravitational to drag force (at a given velocity) for a bicyclist rolling down a hill is approximately proportional to their height, or to the cube root of their weight. (This is yet another example of a square–cube law.)

While this relationship is only approximate (since obviously human bodies are not all the same shape and two equally tall people can have different body weights), it still holds pretty well, especially when comparing a small child to an adult (or an adolescent).

So if e.g. your little sister is 120 cm tall and you're 180 cm, your gravity-to-air-drag ratio at a given speed is about 1.5 times that of your sister (and your equilibrium speed at which drag and gravity are balanced will be about $\sqrt{1.5} ≈ 1.2$ times that of your sister's, assuming a sufficiently steep hill for air drag to dominate rolling drag).

In other words, your dad was right. In an atmosphere, all else being equal, heavier objects really do fall (and roll) down faster.

Answer 2

It is not clear from the description, if the bikes are simply rolling or if the pedals are used. Different gear ratios could easily account for the difference in the latter case, while in the former it is mostly the interplay between friction and the moment of inertia of a rotating wheel (which depends on its size.)

The following image shows forces acting on the wheel rolling downhill:
(image source)

There is a static friction force (denoted as simply Friction force in the image), which is limited by the maximum possible value for no slipping: $$ \text{Friction force }\leq \mu N=\mu Mg\cos\theta $$ If the friction force exceeds the critical value, slipping occurs. As the critical value is not the same for the two bikes, with the riders and the bikes themselves having different masses, slipping of a smaller bike wheels could account for the disparity.

The rolling friction force (named Drag force in the image) is also proportional to the mass: $$ \text{Drag force }=\mu N = \mu Mg\cos\theta, $$ however the friction coefficient itself is dependent on the wheel parameters. Wikipedia even proposes two different formulas for it - inversely proportional to the wheel radius and to the square root of the wheel radius($C_{rr}=\sqrt{z/d}$ and $F=C_{rr}N=bN/r$). This suggests that heavier rider would experience higher friction force... but the numerical value of the prefactor would be also different for the two bikes or even for the identical bikes with the wheels having different pressure.

Finally, when wheel starts rotation, there is friction between the wheel and its axis, in other words, the Newton's equation for the rotation speed would become something like: $$ I\frac{d\omega}{dt}=-\gamma\omega + r\times\text{ Friction force}, $$ where the moment of inertia is proportional to the radius of the wheel squared: $I\propto r^2$.

To conclude: I wouldn't make bets on which bike rolls faster, so I have doubts about the explanation provided in the Q (Once we arrived home our dad told her that there was nothing to complain about as I am heavier than her.) But expecting that they arrive at different times is quite reasonable.

Update
Some of the answers and comments have focused on the air drag, as the main factor slowing down the bikes. IMHO, although the air drag is certainly a factor, claiming that it dominates requires quantitative estimates that no one provided (for the air drag and the alternatives outlined above in this answer.) Without making definitive claims I suggest a few points to consider:

• As bicycles start from zero velocity, I seriously doubt that their speed at the end of the bridge is as high as 20 km/h or more, where the air drag becomes important.
• The linear drag is independent on the mass (see the derivation here and Stoke's law), whereas quadratic drag starts to play role at higher velocities (see terminal velocity.)

Answer 3

It depends. Here are my thoughts: In general, you have to take into account the moment of inertia for rolling objects. The object with a bigger moment of inertia will accelerate slower, if they have the same dimensions, i.e. same shape but different distribution of the mass. For different sized wheels have a look at this post here. The two cylinders with different radii have the same speed for any height $h$. So from that I would conclude that the reason is not different sized wheels.

Regarding the weights: You are right that both of you are accelerated by $g$ in the same way. But in principle, the lighter you are, the more air resitance will play a role. So the final velocity of heavier objects is always higher. Compare a feather falling vs a rock. I am not sure that this is the reason. But you can just check. Let your sister use your bike and see if she is as fast as you or slower. (Compared to you on your bike; take the time) Posture is of course also important regarding the air resitance.

My best guess would actually be that the friction in the bearing is the important point. If it is old bike vs new, then the new one might have a better chance.

Answer 4

Presumably the speeds were rather modest, so ignoring air drag. I have seen something similar when riding with my wife (roughly half of my weight). I cannot vouch for the frictions to be equal (my bike is newer, and probably better maintained). But consider the following effect that kicks in already at the lowest speeds (unlike air drag).

Imagine a rider with mass $M$ on a bike with mass $m$, and wheels with moment of inertia $I$ and radius $R$. The total kinetic energy of this system, travelling at speed $v$ (hence with the wheels rotating at angular speed $\omega=v/R$, no slipping) is $$E=\frac12Mv^2+\frac12mv^2+\frac12(I/R^2)v^2.$$

Assume that all of the gravitational potential energy of the system, $V=(M+m)gh$, $h$ the difference in elevation, is converted into kinetic energy (ignoring friction, too). We arrive at the equation $$ v^2\left(\frac12(M+m)+\frac12(I/R^2)\right)=(M+m)gh. $$ Solving for $v^2$ gives $$ v^2=2gh-\frac{2I/R^2}{M+m+I/R^2}gh. $$

Look at the extra term with the minus sign. It accounts for the difference from free falling from height $h$. With two riders of different masses $M$ on identical bikes (so the same $m, I,R$) we see that the heavier rider ends up going faster simply because with a heavier rider a smaller fraction of the available energy is wasted in the rotational energy term $\frac12I\omega^2$.

---

See the comments by Ilmari Karonen under this answer for an explanation as to why using wheel mass as a substitute for $I/R^2$ is a fair approximation. This leads us to the following way of testing whether this effect is real: two riders of the same size (so equal air drag) roll down a hill. Bike frames are also "equal", but one is riding a regular bike while the other rides a fatbike. Who will win? According to the posters who think air drag is the only factor it would be a draw, right?

Answer 5

This may not be the answer you are looking for on Physics SE, but...

A correct answer that hasn't been posted yet is:

• The smaller bike is a child's bicycle.
• The larger bike is an adult's bicycle.
• Toys for children (that can be ridden) have more friction in the wheels as a safety feature.

Friction is physics... so don't let it be said that there's no physics in this answer :-)

Answer 6

Since you and your sister have different bikes with different wheel sizes, the moment of inertia for the wheels may be different and this will affect the acceleration.

The sum of the forces tangent to the slope give the acceleration of the center of mass:

$$ma_{cm} = mg\sin\theta - F_f$$

The sum of the torques about the center of mass give the angular acceleration of the wheel. The only force that produces torque is the rolling friction:

$$I\alpha = F_fr$$ where I is the moment of inertia and r is the radius of the wheel. For pure rolling (no slipping):

$$ a_{cm} = \alpha r$$ and

$$F_f = \frac{Ia_{cm}}{r^2}$$ Substituting and solving for $a_{cm}$ leaves:

$$a_{cm} = \frac{mg\sin\theta}{m + \frac {I}{r^2}}$$

The smaller the moment of inertia of the wheel, the greater the acceleration of the center of mass.

Most bicycle wheels are not solid disks. They are annular in shape:

The moment of inertia is:

$$I = \frac 1 2 m(r_i^2 + r^2)$$ where $r_i$ is the inner radius of the wheel.

Substituting gives:

$$a_{cm} = \frac{g\sin\theta}{1+\frac 1 2 (1+\frac{r_i^2}{r^2})}$$

Note that the acceleration is not dependent on the mass. All that is needed is to calculate is the radii of the wheels.

My guess is that your bike has both a larger radius and thinner wheels ( rim plus tires) which gives your bike an advantage.

Answer 7

I broadly agree with the other answers, but I think they get into the weeds a bit and this can be explained much more directly. There are 3 forces acting on the bike: gravity, the normal force which keeps the bike from dropping through the ground and friction. $$ \sum F = m \vec a = m \vec g \sin \theta + \vec N \cos \theta - \beta f(\vec v ) $$ The normal force, barring jumps, acts perpendicular to the velocity of the cyclist, so we can ignore it. Gravity and acceleration are both proportional to the mass of the cyclist, but friction is not. We model different frictions in different ways, but it always acts opposite the direction of travel and it is not proportional to the mass. Therefore, when we simplify by dividing by $m$, we find

$$ \vec a = \vec g \sin \theta - \frac{\beta}{m} f(\vec v) $$

that as mass increases, the friction matters less and less. It is not qualitatively important where the friction comes from: I've seen better-skilled child skiers travel much more slowly than their adult counterparts, especially on high snow-friction days. If you were modeling cyclists to get precise and accurate predictions, getting into the weeds with friction would matter, but there are so many variables - bike quality, how well each bike is tuned/oiled, tire profile, drag coefficients, rider profiles ... the full list would be exhaustive. The bottom line is that friction matters more for feathers than bowling balls.