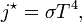One reason is that different parts of the system can be at different temperatures. If a part of the system at $T_1$ transfers an amount $\Delta Q$ of heat to a part of the system at $T_2<T_1$, the hot part's entropy changes by
$$\Delta S_\text{(hot)} = -\frac{\Delta Q}{T_1}$$
but the entropy of the cold part changes by
$$\Delta S_\text{(cold)} = \frac{\Delta Q}{T_2},$$
so the total entropy change is
$$\Delta S = \Delta S_\text{(cold)} + \Delta S_\text{(hot)} = \Delta Q \left( \frac{1}{T_2} - \frac{1}{T_1} \right) > 0. $$
Another reason, as
Ignacio Vergara Kausel pointed out, is that entropy changes can also occur for other reasons than heat flow. For example, chemical reactions can change a system's composition, which affects its entropy.