How this equation arises in free body diagram of rolling motion?

Question

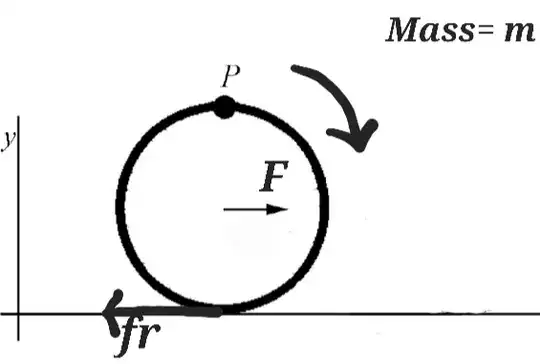
Concerning rolling motion for a sphere (without slipping)

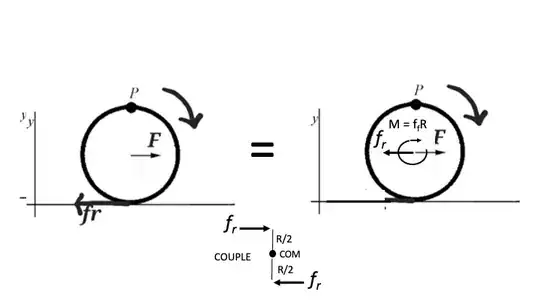
I have read somewhere that here solving using free body diagram we can write$$F-f_r=ma_{com} \space\space\space\space(1)$$ where $a_{com}$ is acceleration attained by centre of sphere i.e its centre of mass, and F acts on centre of mass. And also $$f_r =\tau \space\space\space\space(2) $$ $\tau$ is net torque on sphere.

Though i don't have any doubts regarding (2) but how come (1) is true when both the forces are not acting along same line. Is there some derivation for this if its true or it is not?

Answer 1

You can move a force to another point parallel to its original line of action as long as you add a force couple to account for the torque it applied at its original point of application. That gives you an equivalent force system to the original.

So you can move $f_r$ so that it acts at the center of mass (COM) by adding a couple about the COM equal to $f_{r}R$ where $R$ is the radius.

See the figures below. The force couple $M$ consists of two equal and opposite parallel forces separated by a distance such that they create a pure moment, in this case equal to $f_{r}R$, without any net force.

Hope this helps.