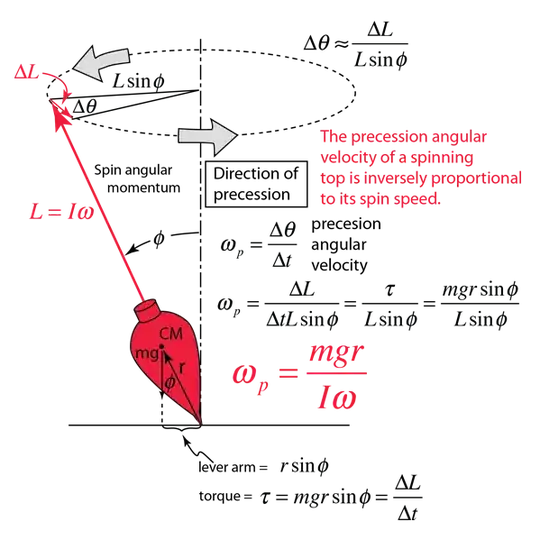
I found many articles with the calculation of the precession rotation speed of the spinning top like this or this. They give this equation for Precession rotation speed $\Omega$: $$\Omega=\frac{mgr}{I\omega}$$
But my question is different. I am not interested in the Precession rotation speed $\Omega$. I am interested in calculating the spinning top rotation speed $\omega$, which is enough, that spinning top is not falling down or precession stays within the specific angle. If I consider this picture:
Then the question can be rephrased like this: What should be the value of $\omega$ (spinning top rotation speed) that angle $\Large\phi$ stays less than some value (for example 5 degrees).
The assumptions:
- I know everything about my spinning top (Moment of inertia, mass, etc.)
- There is no friction.
More specific example: I have a spinning top, which is almost a ring, 10 grams weight, radius 10 cm. Moment of inertia $$I=mr^2=0.01kg \times (0.1m)^2=10^{-4}$$ With which speed (RPS or RPM) I should rotate it, that it's axis stays within 5 degrees to vertical?