Before setting and solving the problem, let's focus on the two main issues of your model:
- you're not considering any gravitational field, $\boldsymbol{g}$, that I'll take uniform throughout the whole space and pointing downwards, $\boldsymbol{g} = -g \boldsymbol{\hat{z}}$;
- you're not using any coordinate to describe the rotation around the vertical axis.

Solving these issues, the Cartesian coordinates of the position and the velocity of the mass become
$$\begin{cases}
x = L \sin \theta \cos \phi \\
y = L \sin \theta \sin \phi \\
z = - L \cos \theta
\end{cases}
\qquad \ , \qquad
\begin{cases}
v_x = L \left( \dot{\theta} \cos \theta \cos \phi - \dot{\phi} \sin \theta \sin \phi \right) \\
v_y = L \left( \dot{\theta} \cos \theta \sin \phi + \dot{\phi} \sin \theta \cos \phi \right) \\
v_z = L \dot{\theta} \sin \theta
\end{cases}
$$
while the kinetic energy becomes
$$ K = \frac{1}{2} m |\boldsymbol{v}|^2 = \frac{1}{2} m L^2\left( \dot{\theta}^2 + \dot{\phi}^2 \sin^2 \theta \right)$$
the potential
$$ U = - m g z = m g L \cos \theta \ .$$
Lagrange equations
$$\frac{d}{dt} \left(\frac{\partial \mathscr{L}}{\partial \dot{q}} \right) - \frac{\partial \mathscr{L}}{\partial q} = 0$$ read
$$\begin{aligned}
0 & = \frac{d}{dt} \left(\frac{\partial \mathscr{L}}{\partial \dot{\theta}} \right) - \frac{\partial \mathscr{L}}{\partial \theta} = m L^2 \ddot{\theta} - m L^2 \dot{\phi}^2 \cos{\theta}\sin{\theta} + m g L \sin{\theta} \\
0 & = \frac{d}{dt} \left(\frac{\partial \mathscr{L}}{\partial \dot{\phi}} \right) - \frac{\partial \mathscr{L}}{\partial \phi} = m L^2 \sin^2 \theta \ddot{\phi} + 2 m L^2 \sin \theta \cos \theta \dot{\phi} \dot{\theta} \ .
\end{aligned}$$
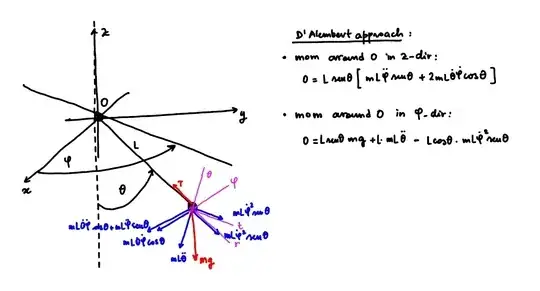
From the point of view of the balance equations of momentum or angular momentum, the former equation is the dynamical equation of the component of the angular momentum orthogonal to the plane identified by angle $\phi$, while the latter equation is the conservation of the z-component of the angular momentum.