5

If the accretion disk surrounds the black hole (like that seen in M87 by the Event Horizon Telescope) but is too far away from the black hole to have its light captured, why do we still see a black shadow? Is the 'shadow' not covered from our perspective by the radiation coming from the accretion disk?

Or does it have to do with the fact that we look at the black hole face on, such that we see the middle of the black hole instead of looking edge-on to the accretion disk only? i.e., When we observe the black hole face-on, the central region of the black hole obscures our view of the background light emitted by the accretion disk and this creates the impression of a dark region or shadow in the center, surrounded by the brighter emission from the accretion disk.

But if this is the case that we look face-on, why don’t we have the large-scale jets ‘in our face’ (discernable on the M87* image of EHT)?

Wikipedia says something about the EHT black hole image: What is visible is not the black hole—which shows as black because of the loss of all light within this dark region. Instead, it is the gases at the edge of the event horizon (displayed as orange or red) that define the black hole. Of course there is hot gas also in front of the black hole, so it’s not immediately obvious why there should be a black core. I think maybe it has to do with much more light emitted around the sides of the black hole reaching the detector at earth than light being emitted from directly in front?

Does it maybe also have to do with the fact that the accretion disk is more like a flat pancake-like shape rather than being distributed spherically around the black hole?

ProfRob
  • 141,325
Jumales
  • 51

1 Answers1

6

The only way we can see to the centre of M87 is if the hot gas surrounding it is optically thin and transparent to its own radiation (NB, and see below, it is likely that the M87 black hole does not possess a geometrically thin, optically thick disk as visualised in the movie "Interstellar"). In those circumstances, then the brightness you see along any particular sightline will correspond to the path length through the hot gas. The brightness in any image will depend on how much emitting plasma is enclosed within the boundary of two sightlines separated by the angular resolution of the image.

If you look directly (radially) towards the centre of the black hole, then your sightline traverses through hot has between about $3r_s$ (the innermost stable circular orbit) and you. This is by no means "black", but in comparison to sightlines which pass close to the photon circle at $r=1.5r_s$ (see below), it is dark.

On the other hand, if you are looking at light arriving with an impact parameter of $3 \sqrt{3} r_s/2$ (basically the radius of the bright ring), then that sightline has a closest approach of $\sim 1.5r_s$, may circle around the black hole and pass through considerably more hot gas. In addition, there is a focussing effect whereby sightlines close to (but greater than) this impact parameter can traverse the surrounding gas at almost any angle, meaning that the summation of all those closely packed sightlines appears very bright.

It is very hard to explain without a picture, so here is one I've borrowed that shows some light rays arising from material around the black hole and heading towards an observer (on the right, at infinity).

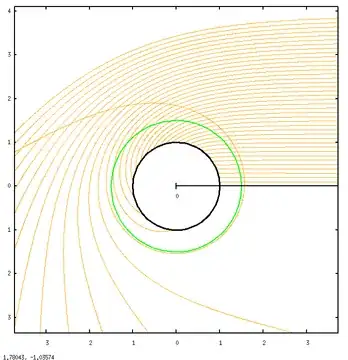
Black hole ray tracing

Any light rays with an impact parameter less than the magic number of $3\sqrt{3}r_s/2$ end up inside the photon sphere at $r=1.5r_s$ (shown in green) and then in the black hole (event horizon is the black circle), so never make it to the observer. The hot gas will only occupy the region further away than $r \sim 3r_s$, which is where the light will originate. You can see there are lots of sightlines encompassing large volumes of emitting material that pass close to $r=1.5r_s$ (but just above) and then end up heading towards the observer with an impact parameter of $3\sqrt{3}r_s/2$ and just above. There are also sightlines directly towards the black hole but these only pass through the material directly in front of the black hole (and at $r>3r_s$) and as a result, this region will appear much fainter.

Edit: It is worth noting that the accretion flow around the black hole is not expected to be in the form of an optically thick, geometrically thin accretion disk - much like that portrayed in the movie "Interstellar" - but a geometrically thick, optically thin (transparent) flow. As the stated in the original Event Horizon Telescope M87 paper:

The simulations of Luminet (1979) showed that for a black hole embedded in a geometrically thin, optically thick accretion disk, the photon capture radius would appear to a distant observer as a thin emission ring inside a lensed image of the accretion disk. For accreting black holes embedded in a geometrically thick, optically thin emission region, as in LLAGNs [low-luminosity active galactic nuclei, like M87], the combination of an event horizon and light bending leads to the appearance of a dark “shadow” together with a bright emission ring that should be detectable through very long baseline interferometery (VLBI) experiments.

In other words, the light coming from around $r=1.5r_s$ is what dominates the image, not the fainter direct light coming from the accretion disk itself. Thus this bright ring morphology would be dominant whatever the orientation of the black hole spin and accretion disk.

ProfRob
  • 141,325