Role of the friction force in rolling without slipping

Question

I don’t understand the following concept and I wonder whether any of you could explain it to me.

Let’s consider a wheel rolling without slipping on a horizontal plane. We only consider the moment when it’s already rolling. Suppose it moves to the right so the only force (except the gravitational and reaction of the ground) acting on the wheel is the force of friction directed to the left. The force of friction provokes a torque so that the wheel is spinning and rolling to the right, but what I dont understand is that while due to the torque the rolling wheel is accelerating to the right, why is the net force directed to the left as it didn’t accelerate but slow down?

Answer 1

To demonstrate how an apparent clockwise torque on an wheel going to the right does not necessarily cause an acceleration to the right, consider the following thought experiment.

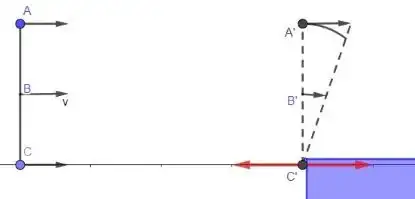
In the diagram A and C are two masses at the nd of a rod that that is moving to the right with velocity v and no friction (e.g. in space) and it has no angular momentum. Imagine it represents two opposing spokes of a wheel. It collides with a massive object and the lower part c' momentarily comes to a stop. The top part A' momentarily continues at the same velocity because it takes a while for the impulse to travel up the rod. As you can see in the diagram the Centre Of Mass (COM) is forced to reduce to half its initial velocity. This represents a backward acceleration of the COM and a corresponding backward linear acceleration. Since force is mass times acceleration this represents a momentary backward force acting on the COM. This makes sense, because the rod system has gained angular kinetic energy and to conserve energy it must lose linear kinetic energy.

Now lets look at it in a reference frame initially co-moving with the rod where it might perhaps be even clearer what is going on.

In this reference frame the massive object moving to the left (representing a road with friction) does impart a clockwise angular acceleration to the rod system, but it can be clearly seen that also imparts a linear acceleration to the left on the COM, which in turn must slow down the linear velocity as seen on the road frame. The take home message is that the 'friction' does not only cause a angular acceleration.

However, once a wheel has gained the correct angular momentum to match its linear momentum, there is no longer any friction between the wheel and road, (if the there is no deforming rubber or a deformation of the road due to weight, which effectively causes an uphill ramp).

Rolling motion does not require friction. Consider a wheel moving and rotating in space. It continues to do that indefinitely without the need for a road with friction. Friction is only required when braking or speeding up, by changing the angular velocity of the wheel. It is also worth remembering that rolling without slipping means there is no net force at the contact point of the wheel, by definition.

Answer 2

The force of friction opposes the direction of acceleration. For a wheel, the point of contact at any given moment in time is not moving w.r.t the surface. If you like, the point is "stationary" and the wheel rotates about that point. This is possible when the force of static friction is sufficient to prevent slipping.

The net force on the point of contact is the torque $I\alpha$ from the spinning minus the force of friction in the opposite direction.

See this answer for example

If there wasn't a torque due to friction, the wheel would just spin in place. Once the friction is sufficient to equal the force/torque from spinning, the wheel continues to spin but without the point of contact "moving" hence why it just rolls about the point.

Answer 3

Let's assume a wheel is rolling without slipping across a horizontal surface.

If it moves with a constant velocity, then the angular velocity, $\omega$, is also constant and therefore both the net force and the net torque are zero. The force of friction on the wheel is therefore zero.

Only when the wheel is accelerating will there be a force of friction acting on the wheel. If, as assumed, the wheel is rolling without slipping, then by that definition, the force is a static frictional force. Where the wheel makes contact with the ground, it is motionless with respect to the ground (just like your shoe when you plant your foot to walk forward).

Figuring out the direction of the static frictional force on the wheel is not trivial. If the wheel is accelerating to the right, then the angular velocity is clockwise and the angular acceleration is also clockwise (the wheel's rotation is speeding up). If friction is the only force causing a torque on the wheel, then the force of static friction must point left, to cause the CW angular acceleration of the wheel.

The description of the previous paragraph is puzzling, though: how can the wheel accelerate forward if the only horizontal force acting is pointing backward? Obviously it cannot be true. I can think of a few ways to rectify this:

1. There could be a forward pushing force, larger than the backwards frictional force, and acting at the center of mass (causing no torque).
2. If the wheel described above is the front wheel of a bicycle, then the bicycle can accelerate because of a forward frictional force on the rear wheel. This is possible on the rear wheel because the chain can provide a larger CW torque on the wheel, such that the net torque (and angular acceleration) from the chain torque and the frictional torque is CW. Of course, for the bicycle to accelerate forward, the (forward) frictional force on the rear wheel must be larger than the (backward) frictional force on the front wheel.
3. If this is a unicycle, then there is an additional torque on the wheel due to the pedals. Then, just like the rear wheel on the bicycle, the pedaling can provide a large CW torque on the wheel, letting the frictional force point forward (with CCW torque). In that way there can be a net forward force on the unicycle (provided by friction) causing it to accelerate, while the net torque is CW, letting $\alpha$ be in the same direction as $\omega$.