A conceptual difficulty about the Ehrenfest paradox

Question

I had always understood that the well-known effects of SR- such as time dilation, length contraction and so on- were properties of the geometry of spacetime so that they applied to spacetime in an abstract sense. For example, the spatial distance between two parallel worldlines in one inertial frame could be length-contracted in another inertial frame. The length contraction could be visualized using the idea of a measuring rod, but in principle, the contraction happens regardless of whether a physical measuring rod is there. The length contraction, in other words, can be considered as simply the result of a transformation between two different coordinate systems.

In a typical explanation of the Ehrenfest paradox, we are asked to consider the circumference of a circle measured out by rods which must contract if they are in motion around the circumference, leaving gaps between the rods, and this is where I have a conceptual difficulty. Suppose we treat the rods as being abstractions. Two adjacent rods can then be considered to be the distances between three points, ABC, where the distance between A and B is the length of the first abstract rod, while the distance between B and C is the length of the second, B being the common point at which ends of the two virtual rods meet. When considered in that abstract sense, there seems to be a contradiction, since if we assume the distance AB is length contracted, and the distance BC is length contracted, then the overall distance AC is length contracted too. There is no way for a 'gap' to open up between the two virtual rods since they share a common point B. We can extend the idea of a succession of virtual rods with common endpoints so that they form a circle, and now there is no way for a 'gap' to appear anywhere on the circumference, which is at odds with the usual explanation of gaps appearing between physical measuring rods. How do I reconcile the two?

Answer 1

The Ehrenfest paradox is resolved by examining the effect of the tilting of the spatial axis at each point on the circumference. If we consider a spacetime diagram that extends the disc into a cylinder along the time axis, and draw the space and time axes of the moving frame at each point, and try to extend them to the rest of the cylinder, we find the spatial axis defining "now" no longer joins up in a circle, but instead is offset in time, so it forms a helix. The length of one turn of the helix is different to the circumference of the circle, but the spacetime volume occupied by the stationary and moving disc is exactly the same.

Moving now to the example of the accelerating rods around the circumference, we have to be careful what we mean when we talk about uniformly accelerating them. Uniform acceleration as measured in the static frame is not uniform in the accelerating frame, because events that are simultaneous in the static frame are at different times in the accelerating frame. If we suppose the idea is that these rods are measuring length in the accelerated frame, and so retain a fixed length in the accelerating frame (this is called "Born rigidity") then the ends follow hyperbolic paths in spacetime with the same lightspeed asymptotes. That is, in the static frame the front and back ends accelerate differently.

The diagram below shows static rods along a line all start to accelerate in a Born-rigid way at the same moment. The "rungs of the ladder" joining the curves show the local "now" (the local spatial axis) in the moving frame. You can see the gaps open up between the rods, but the rods all have constant length in the moving frame.

We can wrap that around a cylinder to see the corresponding behaviour for the Ehrenfest disc. We have various "lengths" measuring the circumference - the lengths in the static frame, the sum of the lengths in the moving frame chosen at a particular static instant, and the length of one loop of the helix in the moving frame. They are all different, but they are allowed to be because they are tilted differently in spacetime. And they all fit on the surface of exactly the same cylinder of events in spacetime.

Answer 2

When considered in that abstract sense, there seems to be a contradiction, since if we assume the distance AB is length contracted, and the distance BC is length contracted, then the overall distance AC is length contracted too. There is no way for a 'gap' to open up between the two virtual rods since they share a common point B.

This is correct. That is, in fact, a contradiction. The solution is to recognize that what happens to AB and BC and AC is not length contraction. It is fundamentally something different. Here are some of the differences:

1. there is no material strain associated with length contraction, nor for Born rigid linear acceleration, but there is unavoidable material strain in angular acceleration.

2. length contraction is symmetric. Each frame sees the other’s rods as being contracted. In rotational motion it is asymmetric. Both frames identify and agree which frame is actually rotating.

3. length contraction is a feature of the Lorentz transform, but the relationship between the rotating and non-rotating frames is not given by the Lorentz transform.

4. The metric has a different form when expressed in rotating coordinates vs inertial ones.

For these reasons (and probably others) it is simply wrong to lump what happens in a rotating frame together with the concept of “length contraction”. They are mathematically, theoretically, and physically distinct. Treating them the same will inevitably lead to contradictions such as the one you identified.

The big issue with rotation is simultaneity. When you talk about length contraction, length is defined as the distance between two points at a given moment of time. In inertial frames we can use the standard Einstein synchronization to define a given moment of time and therefore to define length.

This process does not work in a rotating frame. When you perform Einstein synchronization on neighboring clocks in a rotating frame and continue around the circle, you wind up with a gap. There is a clock whose left neighbor and right neighbor disagree.

So the natural simultaneity convention in an inertial frame doesn’t work in a rotating frame. Hence length has a different meaning in a rotating frame than in an inertial frame.

To avoid this issue we can focus instead on tensor quantities. In particular we can treat the collection of rotating observers as a congruence. This has the effect of allowing us to make coordinate independent descriptions of the geometry of these rotating observers.

If you have observers that start at rest and then undergo angular acceleration, then in a frame-independent sense they will have a positive expansion scalar. Meaning that they will physically get further apart from each other. This physical stretching is directly measurable with local strain gauges and thus is distinct from length contraction which produces no such strain.

Answer 3

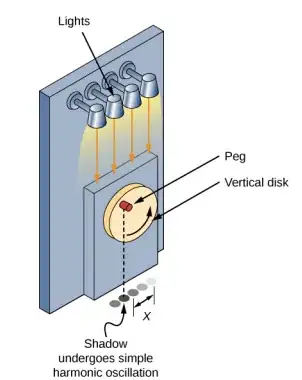
First I will try to convince you how gaps can appear the linear case, which is less contentious.

In the above diagram the two objects (which are initially adjacent to each other with no gap) are individually accelerated in a Born rigid manner so that they are allowed to length contract naturally and maintain a constant proper length in their rest frames. Each object has the same proper acceleration as the other, at any instant in the original inertial reference frame. The front of the blue train accelerates the same as the front of the green train and the same for any part of the trains. The centre to centre (or back to back or front to front) distance remains constant at any instant in the original inertial reference frame. As can be seen (red segment) a gap opens up which can be larger than the length of the objects themselves. This is simply what physically happens and what can be measured, fully in accord with Special Relativity.

You can imagine drawing many of these trains end to end in a straight line on paper and then rolling the paper into a cylinder. You will then end up with something that looks very much like the last two diagrams posted by Nullius. The main difference is my diagram shows the instantaneous length measured by the inertial observer that does not accelerate, while his diagrams show the tilted lines of simultaneity of the segments. Strictly speaking the lines of simultaneity should tilt the other way, due the rear of the segments accelerating faster than the front of the segments and traveling further through space time.

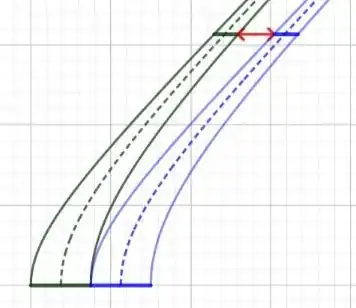
Now for the circular case:

As can be seen the circulating trains individually length contract with increasing inter train gaps, just as in the linear case. Due to the Born rigid acceleration, the individual circulating trains maintain their proper length at all times during the acceleration phase.

It can be shown that accelerating each train with equal proper acceleration is the natural behaviour. Consider Einstein's rotating disk. If rulers are pinned on the periphery at their front ends and the trailing ends left free to length contract, when the disk is spun up, each ruler will experience the same proper acceleration at any instant at the pinned end. In fact the any point on a given ruler will experience the same instantaneous proper acceleration as the equivalent point on any other ruler on the periphery.

As for concerns about centripetal and centrifugal forces this can be made negligible. The proper centripetal force experienced by observers riding on the trains is $$F_c = \gamma (m \omega^2 R) = \frac{m v_t^2}{R\sqrt{1-v_t^2/c^2}}$$ where $v_t$ is the instantaneous tangential velocity. For a constant final tangential velocity, the only variable is $R$ and the centripetal force can be made arbitrarily small by making $R$ arbitrarily large.

In the animation all the trains (linear and circulating) maintain the same length as measured by comoving observers and there is no stress or strain parallel to the motion due to the Born rigid acceleration.

The circulating trains animation also illustrates another relativistic concept, the "Momentarily Comoving Inertial Frame MCIF". This concept allows SR to be extended to handle accelerating objects, and says that over a small enough temporal and spatial interval the time dilation and length contraction of an accelerating (linear or circular) object is exactly the same as that of an inertial reference frame that is momentarily comoving with an infinitesimal part of the object. This equivalence of the length contraction of the linear and circulating trains can clearly be seen in the gif, even during the acceleration phase.

Its not hard to imagine that if the circulating trains were connected with thin elastic bands, the bands would be stretched and have a measurable tension. If the four trains are connected by inelastic couplings, it is easy to see that the trains would be stretched in the their own rest frames and under enormous tension. This is why reason the Ehrenfest cylinder is considered to have to physically deform when its angular velocity is increased.

Another thing to bear in mind is that while SR can handle acceleration, the standard Lorentz transforms cannot. The standard transforms assume the observer and observed object have had constant velocity relative to each forever, In the accelerating cases, it is important to take into account whether it was the observer or the observed that accelerated. For example, if I accelerate relative to another rocket, reach a constant velocity and resynchronise my clocks, I will observe the clock at the rear of the unaccelerated rocket to be ahead of the clock at the front exactly as predicted by the Lorentz transform. Now if I remain stationary and observe the other rocket accelerate to a final constant velocity, the clocks at the rear of the accelerating rocket will be retarded instead of advanced, relative the clocks at the front. This is because after the accelerating rocket has accelerated, the rear of the rocket has travelled further than the front of the rocket due to length contraction and the clock at the rear will have experienced more time dilation.

Edit: While measuring 'global' distances in a rotating frame is difficult due to being unable to synchronise the clocks all the way around, it is possible to make sensible local measurements for a cylinder with constant angular velocity. For example, we could place a ruler on the rim of the Ehrenfest cylinder and we can place clocks at either end of the local ruler. It is possible to synchronise the clocks locally. We can then measure the radar length of the ruler and find the local radar length is the same whichever end we measure from. This local radar length is the proper length of the ruler.

A final thought. Imagine the rulers on Einstein disk are pinned at both the front at back while the disk is stationary. As the disk is spun up, the rulers are force to maintain the same length measured in the inertial reference frame of the observers outside the disk. This means the proper length of the rulers is stretched in their own reference frame as measured by comoving observers on the rotating disk and they come under tension just as the string does in Bell's rocket paradox.

Answer 4

Uniform circular motion along the circumference and motion along the diameter while it is spinning are two different reference frames:

1. Motion along the circumference can be treated as an inertial frame.

The tangential velocity along the circumference is constant and there is no tangential acceleration. All the acceleration is centripetal and is uniform at all points of equal radius. If half a circumference C is stretched into a straight line then the centripetal acceleration will resemble a constant acceleration along the the straight length (like gravity) If the stretched line exerts a constant normal force that counters the centripetal acceleration, then the sum of the acceration is zero.

Now all the requirements for an inertial frame have been met so for relativistic tangential velocity $$C' = \frac{C_o}{\gamma}$$

2. Motion along the diameter of a circle exhibiting uniform circular motion is a non-inertial frame of reference.

Any motion along the diameter has a constantly changing centripetal acceleration parallel to the direction of motion which is maximum at R and approaches a minimum (0) as one approaches the center. The motion along the diameter is identical to the motion of the amplitude of a sine wave (Simple harmonic motion) and can be modeled as rotational motion by looking at the shadow of a peg on a wheel rotating at a constant angular frequency.

The motion along the radius can be expressed as $x(t)=Acos(ωt)$

If there is a full special relativity solution to the Ehrenfest paradox, it is in the proper treatment of the measurement of length or motion along the diameter such that the problem can be expressed in an inertial frame of reference.