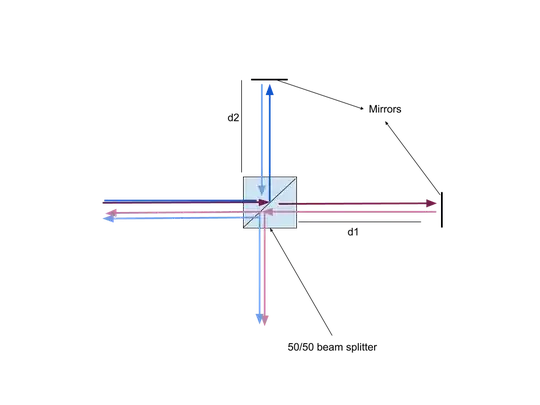
So based on @Quantum Mechanic 's answer, I've tried to come up with an answer to the question. I will be using this revised diagram:
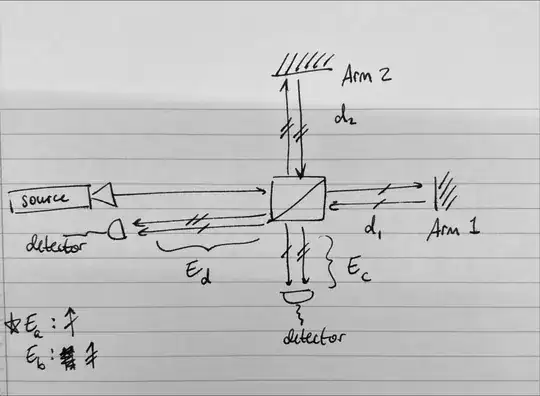
Step 1: light exits source and hits beam splitter
We will assume the light that exits the source will have amplitude $E_0$ (specifically, $\vec{E}_{source}(x,t)=E_0cos(kx- \omega t)\hat{e}_x$, but this specificity isn't too important to this answer). We can use the 50/50 beam splitter matrix equation to calculate the intensity of light that will hit the mirrors labelled "Arm 1" and "Arm 2" respectively (this equation is inherent to the 50/50 beam splitter, and simply describes how the phase of the beams are affected by the splitter itself):
$$\begin{bmatrix}E_{received,\ arm\ 1}\\E_{received,\ arm\ 2}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}E_0\\0\end{bmatrix}$$
Note the use of $\begin{bmatrix}E_0\\0\end{bmatrix}$, where the second component is 0. This because all of the electric field is entering through one input port, not both. Computing this matrix multiplication, we arrive at the conclusion that
$$\begin{bmatrix}E_{received,\ arm\ 1}\\E_{received,\ arm\ 2}\end{bmatrix}=
\begin{bmatrix}\frac{1}{\sqrt{2}}E_0\\\frac{1}{\sqrt{2}}E_0\end{bmatrix}$$
Knowing intensity goes as $I \propto E^2$, we can say
$$\begin{bmatrix}I_{received,\ arm\ 1}\\I_{received,\ arm\ 2}\end{bmatrix}=
\begin{bmatrix}\frac{1}{2}I_0\\\frac{1}{2}I_0\end{bmatrix}$$
Step 2: light reflects off mirrors and hits beam splitter again
When the light received by arms 1 and 2 reflect off the mirrors and arrive back at the beam splitter, note that we will be dealing with two incident electric fields -- I will call the one coming from one of the arms $E_a$ and the other $E_b$. It doesn't really matter which is which, but it does matter that one of the arms is movable -- that is, $d_1$ isn't always equal to $d_2$. This is key. Let's say $d_1$ is such that when light hits it, the light is reflected exactly in phase. That is,
$$E_{b}=E_{received,\ arm\ 2} cos(kx - wt) + E_{received,\ arm\ 2} cos(kx + wt) = 2E_{received,\ arm\ 2}cos(kx-wt) $$
However, let's say this is not the case for $d_2$. Specifically, let's say $d_2$ is such that when light bounces off the mirror, it is reflected with a new phase, $\varphi = kx + wt + \phi$.
$$E_{a}=E_{received,\ arm\ 1} cos(kx - wt) + E_{received,\ arm\ 1} cos(kx + wt + \phi) = 2E_{received,\ arm\ 2}cos(kx-wt)cos(\phi) = cos(\phi)E_b$$
Plugging this into our beam splitter matrix equation:
$$\begin{bmatrix}E_{received,\ det\ A}\\E_{received,\ det\ B}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}E_b\\E_bcos(\phi)\end{bmatrix}$$
We get that
$$\begin{bmatrix}E_{received,\ det\ A}\\E_{received,\ det\ B}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}E_b(1+cos(\phi))\\\frac{1}{\sqrt{2}}E_b(1-cos(\phi))\end{bmatrix}$$
Finally, plugging in the subtle implicit conversion we did earlier: $E_b=\frac{1}{\sqrt{2}}E_0$:
$$\begin{bmatrix}E_{received,\ det\ A}\\E_{received,\ det\ B}\end{bmatrix}=\begin{bmatrix}\frac{1}{2}E_0(1+cos(\phi))\\\frac{1}{2}E_0(1-cos(\phi))\end{bmatrix}$$
This is our final solution. Note that this works in all of the observed cases, for example:
- $\phi = 2\pi n + \pi$: all of the light goes into detector B, and none into A
- $\phi = 2\pi n$: all of the goes into detector A, none into B
- $\phi = \frac{n \pi}{2}$: half of the light goes into detector A, half into detector B