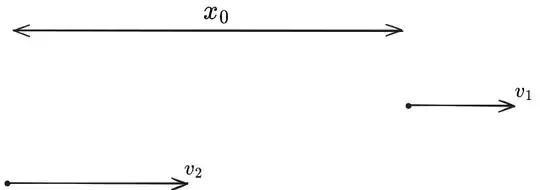
Lets say there are 2 point particles A and B separated by a distance $x_{0}$ whose velocities are $v_{1}$ and $v_{2}$ along the positive X-axis respectively such that $v_{1}>v_{2}$
We can clearly see that at some time, A will over take B.
Now we consider the exact scenario in a different way.
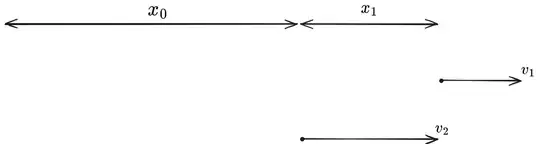
A covers $x_{0}$ in $t_{0}s$. In the $t_{0}s$, B covers a distance $x_{1}$. A covers $x_{1}$ in $t_{1}s$ and so on. Now every time A reaches B's old position, B has already moved forward from there.
After a while, $x_{n}$ is very small but still not 0. Then how exactly does A overtake B?