When not pedaling, the friction force on the wheels of the bicycle is directed backwards, but doesn't this give the tires angular velocity?

Question

The bicycle in the figure gained speed and then the feet were pulled back from the pedals. Since no torque is applied to the pedals, the friction force on the rear wheel is directed backwards. However, after this point, there is something that confuses me. Friction forces create a backward acceleration that slows down the object. But the same friction forces cause the wheels to gain angular velocity clockwise. Won't this cause the wheels to spin faster? How will the speed of this bike be 0(zero)? Can you explain with drawings?

EDİT:

I edited my question. I found that the factor that slows down the angular velocity of the wheel is the normal force.

$N.d > {{F_s}_1}.r $

HC Verma- concepts of physics page 183

Answer 1

Practically there is not just point of contact between the tyres and the road but rather an area of contact which is due to the deformation of the tyres. Due to this deformation the normal force acts slightly out of line from the center of mass. This produces a backward torque that reduces the angular velocity.

And the frictional force will be $\bf non-zero$ unlike what most comments state.

For more information refer to HCV concepts of physics part 1 page number 183

Answer 2

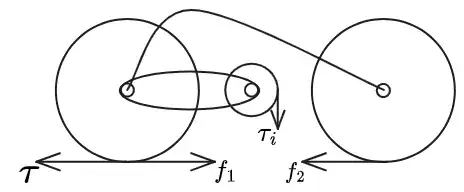
When we are pedaling, a torque $\tau$ is induced in the wheels of the cycle. Since the tires generally have a good traction with the road, the friction force acting on the cycle would be $f_1 = \frac{\tau}{r}$ where $r$ is the radius of the wheel. $\tau_i$ is the torque induced on the pedal by your foot.

Since, generally the pedal is connected to the back tire, the torque acts on the back tire and causes the motion. This causes the front tire to slip and hence, a friction force $f_2$ acts on the front wheel, making it rotate.

Now when you stop pedaling, there is no torque acting on the wheel and the wheel is pure rolling. $v = \omega r$ where $v$ and $\omega$ are velocity and angular velocity respectively.

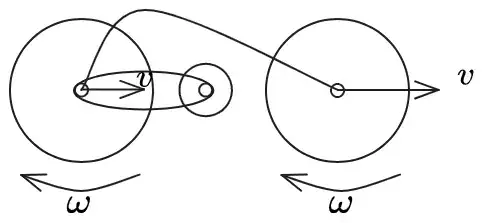
When the wheels are pure rolling, the friction force acting on the bike would be $0$ and ideally, the bicycle keeps rolling forever. But generally, when we stop pedaling, the bicycle comes to a stop after going for a bit.

This is due to other dissipative forces such as friction in the bearings, resistive forces in the sprocket and rolling friction. These resistive forces acts on the cycle which brings it to a stop.

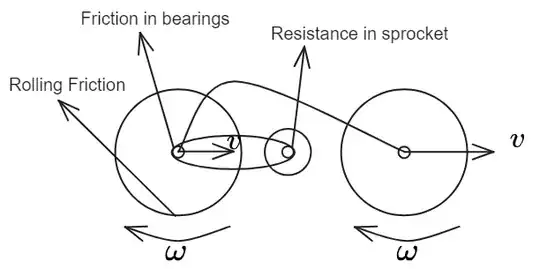
The friction force isn't the force that brings the bicycle to a stop. it is the internal resistive forces and rolling friction that brings the cycle to a stop and these forces actually slow down the wheel rather than make them spin faster.

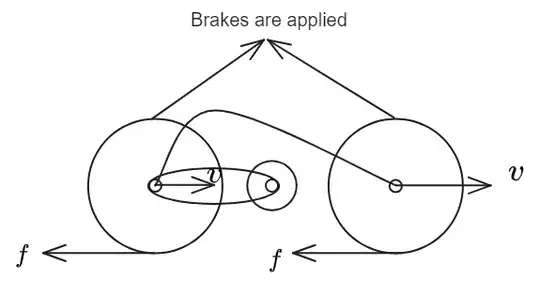
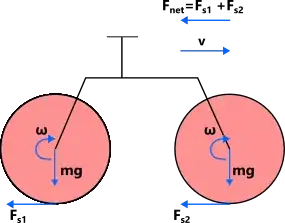
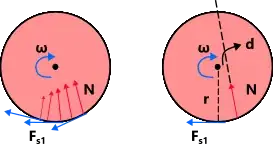
When we apply the brakes, the wheels are forced to stop spinning while the bicycle continues to move forward. hence a friction force $f$ acts on the tires opposite to the direction of motion, thus stopping the bicycle

Answer 3

It is not friction at the contact point of the wheel that slows the wheel down and the friction does not give the wheel angular velocity.

The main cause of the slowing down is due to the hysteresis of a rubber tyre and due to the reaction force from compressing the rubber tyre in front of the wheel.

In the diagram above the hysteresis of the tyre is greatly exaggerated for clarity. As the wheel rolls to the right and compresses the tyre in front of the contact patch there is a reaction force at A. This reaction force produces an anticlockwise torque about the contact patch B which acts as a fulcrum.

There is no net force at point B. If there was a net force at B, the tyre would skid relative to the road but that is not happening in the free rolling case. Non zero net force always produces motion. The torque produced at A becomes a torque at point C which in turn produces a rearwards force at the wheel axis C. Since there is no net force at B, there is no angular velocity imparted to the wheel in either direction by friction at the contact point.