One reason the Schwarzschild metric is so well known, is because it was the first exact solution found for a gravitational body in General Relativity, and even Einstein did not think an exact solution was possible.
Even more remarkably, Schwarzschild found the solution while serving on the Russian war front and only a few months after Einstein had published his theory of General Relativity.
Now why does this event horizon or singularity disappear in a different set of coordinates? One way to visualise this is to consider the analogous Rindler Metric.
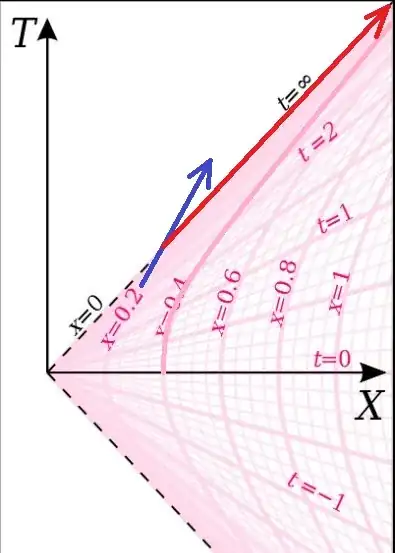
This is set in flat spacetime with no gravity involved. The Rindler observers are a set of observers (the hyperbolic curved pink world lines) accelerating in flat spacetime in such a way that they consider their spatial separation to be constant. An artificial event horizon is visible to them (the diagonal dashed black $x=0$ world line). The $X$ and $T$ coordinates are the normal coordinates of an inertial observer in flat spacetime, observing the observers accelerating relative to her.
If an observer falls off one of the accelerating rockets, she follows a straight trajectory (the blue worldline) in flat spacetime and passes through the apparent event horizon. Her colleagues on the accelerating spaceships never see her pass through the event horizon because light rays from the crossing event (the red wordline) never reach the accelerating rocket observers (e.g. the pink worldline of the observer at $x=0.4$).
Any inertial observer in the flat spacetime does not see any event horizon and nothing unusual about the location. However, just like falling into a black hole, once the observer crosses to the left of the apparent event horizon, he can never cross back to the right side of the apparent event horizon, because he would have to exceed the speed of light to do so. Also, just like a black hole, before he crosses the event horizon, the accelerating Rindler observers see light coming from the falling observer as progressively more red shifted due to their own acceleration.
To the accelerating rocket observers, the event horizon is real because they can never see anything behind it. To the rocket observers the falling observer seems to take forever to reach the event horizon and they never see him cross it. On the other hand, the falling inertial observer just passes straight it and the trip only takes a few minutes by her watch.
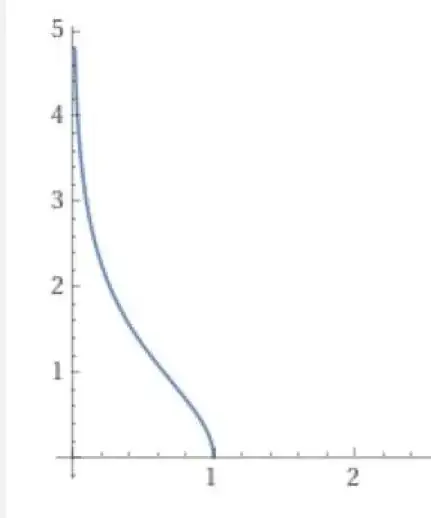
The chart below is the point of view of an accelerating observer that was initially at $X=1$. The vertical axis at $X=0$ is the apparent event horizon. This accelerating observer sees the free falling observer as following the curved blue world line that asymptotically approaches the horizon, never quite stopping and never reaching the horizon.
The equation for the curve is $$t = \cosh^{-1}\left(\frac{X}{x}\right),$$ where $X$ is the initial height of the falling object, $x$ is the height at time $t$ and $t$ is the proper time according to the clock of the accelerating observer.
In the next chart, the vertical axis is the velocity of the free falling observer as seen by an accelerating observer and the horizontal axis is now the proper time of the accelerating observer:
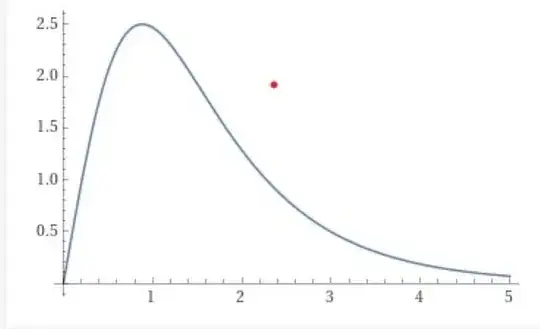
The accelerating observer sees the falling observer rapidly accelerate at first and then slow down, but again he never sees her come exactly to a stop, but this motion is eventually so slow that it appears to be "frozen". The motion is described by the equation $$v = X \times \frac{\tanh(t)}{\cosh(t)},$$ where $X$ is the initial height of the free falling observer at $t=0$ and $t$ is the proper time of the accelerating observer. As $t$ approaches $\infty$, the observed falling velocity asymptotically approaches zero.
The equations used in the charts can fairly easily be derived from:
The Relativistic Rocket Equations (Baez).
The Rindler Coordinates (Wikipedia)


