Is there a force associated with relativistic length contraction?

Question

EDIT: It appears there is a position taken by some, that there is no force measured and the chain drive does not shorten at all, however fast the chain is moving in the lab. I would genuinely appreciate thoughts, opinions and feedback on this alternative position.

While putting together an answer for this question "Relativistic Chain Drive Paradox" it occurred to me that the set up provides a really good demonstration of the physicality of length contraction and can also demonstrate that it is associated with a real force. The Bell Rocket ships paradox does the same, but this mechanism could in principle be set up in an Earth lab and demonstrate length contraction that can be measured by a static ruler in our own reference frame and observed to occur right before our very eyes.

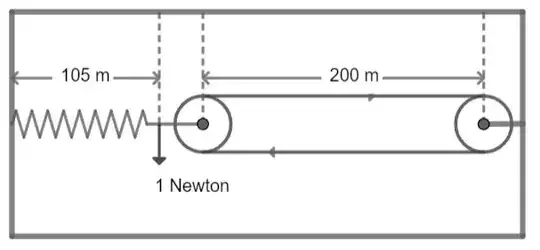
The slightly modified set up (Illustrated above) requires a driven gear with a fixed axle and an idler gear that that keeps the chain drive under a small tension due to being attached to a spring balance which is attached to something solid like a wall. We now turn on the gear drive and observe the chain contract to say half its stationary length. The tensioning spring balance was initially reading say 1 newton, but at full speed the balance is reading a greater force.

Edit: I moved my self answer to here to show my attempt at an answer. The calculations are now less relevant as the question has become is there any force of contraction observed at all?

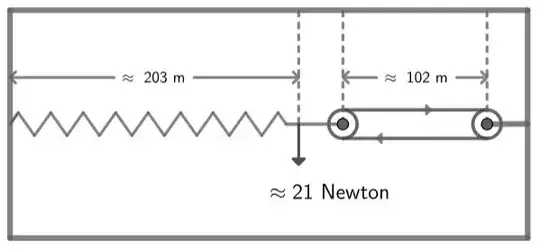
Assume the spring constant of the spring is $0.2 N m^{-1}$. It is initially set up with a tension of 1 newton so it has a length of 105m when set up. Assume the chain links have a spring constant or stiffness of $10 Nm^{-1}$ and the distance between axle centres of the pre-tensioned chain drive is 200m. This means the un-tensioned length of the chain drive is 199.9m. Now we start the drive gear and accelerate the chain up to a constant speed of $v = \sqrt{3/4}$ as measured in the lab, such that the gamma factor $g = 1/\sqrt{1-3/4} = 2$ using units such that c = 1. The chain drive now looks like this:

Notice that gear wheels themselves have been allowed to shrink by a factor of approximately 2 along with the chain itself. The force on the spring balance is $F_s = k_s d_s$ where $k_s$ is the stiffness of the spring and $d_s $ is the displacement of the spring. $d_s$ in turn is defined as $(L_s -$ un-tensioned length of the spring), where $L_s$ is the current tensioned length of the spring. $F_s = k_s d_s = 0.2 (L_s - 100)$ The balancing force on the chain drive is correspondingly $F_c = k_s d_s$. We have to remember to divide the relaxed length of the chain drive by 2 due to the length contraction factor so $F_c = k_c d_c = 10 (L_c - 199.9/2)$ Since the system is in equilibrium $F_s = F_c$ and $0.2 (L_s - 100) = 10 (L_c - 199.9/2)$ The total length of the chain drive and the spring scale was initially 105 + 200 = 305 and the total remains the same after the chain drive starts operating so we can say $L_s + L_c = 305$. We now have 2 unknowns and 2 equations so it is a simple simultaneous equation, and the solutions for the lengths of the spring and the chain drive are $L_s \approx 202.99m$ and $L_c \approx 102.01$ as in the diagram. The force indicated on the spring balance, while the drive is operating is $F_s = k_s d_s = 0.2 (202.99 - 100) \approx 20.598 N$. Note that while the gamma factor is 2 the chain did not quite contract by a factor of 2, due to the tension on the chain.

P.S. Ignore contraction of the gears themselves. Assume they have been engineered to reduce their diameter as required while not affecting the length of the chain.

Answer 1

The fact that the belt is a moving loop means that it would be simpler to examine in the rotating frame. This thought experiment is basically the same as the famous rotating disk problem that Einstein discussed in 1909 towards the beginning of the development of GR. The difference in shape is not an obstacle, but the many papers on the rotating disk are valuable to understand the physics at play. Einstein noted that the observer in the rotating frame would need more meter sticks to measure all the way around the circumference. And, the meter sticks would look shortened in the non-rotating frame. This is understood now as non-Euclidean space exists in rotating frame and the formula for the circumference of a circle in that frame is $ 2 \pi r/(1 - r^2 \omega^2/c^2)^{1/2}$. The angular velocity is $\omega$. The radius is unchanged because it is perpendicular to the motion.

For many years there was a paradox about what happens when a disk is sped up. There is not enough material in the disk to go around the circumference and so it would need to squeeze the radius smaller. But, what if the disk were made of infinitely rigid material. Then an infinite force would have to exist to squeeze it and infinite energy would be needed. Where would that energy come from? Could it come from the energy required to spin the disk? How could internal energy affect the rotational inertia sufficiently? The stresses would increase the stress energy tensor, but the energy created is more than the energy needed to rotate that energy.

The resolution is that you cannot forget about the centrifugal accelerations because they dominate in real materials, and infinite rigidity is impossible because it results in a speed of sound in the material greater than the speed of light. For all physically possible materials, the expansion from centrifugal accelerations exceed the non-Euclidean contraction. For material with sound speed at the speed of light, the two are equal. There is never a squeezing down from contraction, and energy is not expended in contraction. In the rotating frame, there are two fictitious forces countering each other. Clark (1949) taking into account elastic effects found the change in radius to be $$ \Delta R = \frac{R_0^3 \omega^2}{8}\left(\frac{1}{c_0^2} - \frac{1}{c^2}\right)$$ where $c_0$ is the sound speed in the material.

McCrea (1971), following Brotas and Cavalleri, included density increases due to higher strains and found that the radius grows with rotation speed for the maximal rigid material up to $R_0 \sqrt{2}$.

Changing the set up to a long straight path with two quick turn arounds at each end does not change the final outcome. The accelerations at the end are sufficient to stretch the material enough to undo the Lorentz contraction no matter how long the belt is. The spring will contract rather than stretch.

I don't disagree with Ocram's answer that if you want an object contracted by its velocity to regain its rest frame size, a force is needed to stretch it. Classically, one can point to the fact that the outward stretching of a belt from centrifugal force is reduced by the Lorentz contraction to argue that there is a force. But, in GR these are both due to warping of space-time.

Answer 2

I suggest the best way to conceptualise this is to consider that an object has its proper length in its rest frame, and occupies a shorter space in any other frame. If you want to constrain an object so that it occupies its natural proper length in a frame in which it is moving, you have to stretch it in its rest frame, which requires a force. That is what happens in Bell's spaceship paradox, causing the strings to break.

The key point that a moving object will be length contracted in the absence of any applied force, but an applied stretching force will be required to combat the effect of length contraction, and the moving object will resist the applied stretching force with an equal and opposite tendency to contract back to its natural proper length in its rest frame.

Answer 3

I apologize for posting many answers, if that's a bad thing.

Let's say a spaceship hovers near black hole horizon, a few millimeters away from it. There is a large difference between acceleration felt at the lowest part of the spaceship and at the highest part of the spaceship. (If that is not clear for anyone, then I recommend posting a question to this site)

Let's say it's such spaceship that the rockets are pulling instead of pushing.

Now we move the spaceship to empty space, while keeping the motors thrusting the same way as before (as measured locally inside the spaceship).

Equivalence principle says that there is still a large difference between acceleration felt at the lowest part of the spaceship and at the highest part of the spaceship.

A simple accelerometer measures how large is the force that is pulling a mass hanging on a spring.

So a mass placed low in the space ship accelerates more than mass placed high in the spaceship.

So the mass hanging low in the space ship approaches the mass hanging high in the spaceship.

So in this case a force difference is associated with decreasing of distance, in accordance to length contraction. And force difference is caused by length contraction of the spaceship.

Answer 4

When a long object (like a chain or a spaceship) accelerates, there is a time difference between the front and back. The watches of passengers in an accelerating spaceship will show different times. This results in the length of the accelerating chain not changing. (It is a bit complicated.) It is like the Bell spaceship paradox, where the distance between the two accelerating spaceships remains constant.

Answer 5

Alright, let's tackle this intriguing question with a bit of a deep dive but keeping it as approachable as possible. The heart of the matter is whether relativistic length contraction, a prediction of Einstein's Special Relativity, is associated with any real, measurable force.

First off, it's key to understand that length contraction is a result of objects moving at significant fractions of the speed of light relative to an observer. This isn't something we encounter in everyday life, but rather a fascinating phenomenon that becomes apparent at very high velocities. Now, onto the force part.

The essence of your question revolves around scenarios like the "Relativistic Chain Drive Paradox" and "Bell's Spaceship Paradox," where length contraction could, theoretically, exert forces on physical objects, potentially leading to measurable effects like tension changes in a chain or string.

In classical mechanics, force is typically associated with mass, acceleration, or some form of physical interaction like electromagnetic forces. However, in the realm of special relativity, things get a bit more nuanced. The concept of force still exists, but how it's applied and observed can drastically change due to the relativistic effects on space, time, and mass.

When discussing relativistic length contraction and forces, we're venturing into a domain where the geometry of spacetime itself is altered by velocity. The "force" observed, such as an increase in tension or a string breaking in Bell's Spaceship Paradox, isn't a force in the traditional Newtonian sense but rather a result of differential length contraction across an object or system. This contraction doesn't directly apply a force but results in conditions where, from the perspective of an observer in a different inertial frame, it seems like forces must be at play to account for the observed effects.

The critical takeaway here is that while we might not describe these outcomes in terms of conventional forces acting upon the objects, the effects—such as increased tension or breaking strings—are real. They are manifestations of the fundamental changes in spacetime geometry that special relativity predicts for objects moving at relativistic speeds. These phenomena highlight how, in the relativistic framework, our intuitive notions of space, time, and force require careful reconsideration to fully grasp the implications of Einstein's theory.

So, in a way, yes, there is a "force" associated with relativistic length contraction, but it's not a force in the way we usually think about pushing or pulling on objects. Instead, it's more about the relativistic effects themselves causing conditions that lead to observable outcomes, which we then interpret through the lens of force and tension. This perspective shift is what makes studying relativity both challenging and incredibly fascinating, as it pushes the boundaries of how we understand the physical universe.