Consider a spin Hamiltonian. I am interested in understanding how the spin-spin correlation function $C(r_{ij}) = \langle \boldsymbol{S}_i \cdot \boldsymbol{S}_j \rangle - \langle \boldsymbol{S}_i \rangle \langle \boldsymbol{S}_j \rangle$ relates to whether or not the system is gapped or gapless. Given the system is in some phase (no phase transition), the correlation function can decay exponentially or according to some power law.
- Is the statement “correlation function decays exponentially” equivalent to saying the spectrum is gapped? I.e. are implications in the figures below directional? Similarly for power-law decay and gapless spectrum. Note, unlike the question here, I am staring with a Hamiltonian.
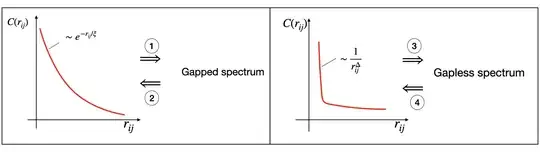
What is the physical argument for the connection?
Attempt: the correlation function tells us the likelihood of a spin at site-$j$ pointing opposite or similar to a spin at site-$i$. If there is strong correlation (exponential decay not power law), then it costs a finite amount of energy to flip a spin at site-$j$ relative to site-$i$ and excite the system. On the other hand, for weaker correlation (power law), we can find an arbitrarily small energy that can flip a spin at site-$j$ relative to site-$i$.
Does the above argument change if the ground sate is degenerate?
Suppose we calculate the spectrum using Exact diagonalization or DMRG. Given that the spectra of all finite systems are gapped, how do we check whether the Hamiltonian is truly gapped or if it is due to finite size effects? Aside: for a 2D system with $N = L_x \times L_y$, which is the relevant dimension to check $\Delta E$ vs $1/L_y$ (say if we change $L_y$) or $\Delta E$ vs $1/N$?
Is this a “robust” way to determine whether or not a given phase is gapped/gapless? That is, are there cases like spin-liquids or 1D systems where correlation function gives us inconclusive answers? Any reference to elementary texts is greatly appreciated.