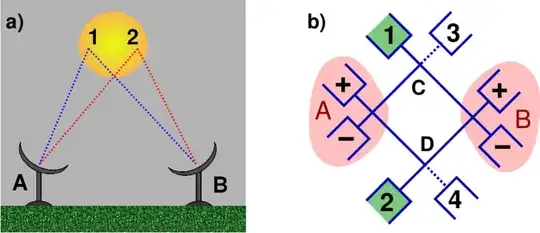
For details, see the book Hanbury Brown: "THE INTENSITY INTERFEROMETER: Its Application to Astronomy", Robert Hanbury Brown, Taylor&Francis, 1974
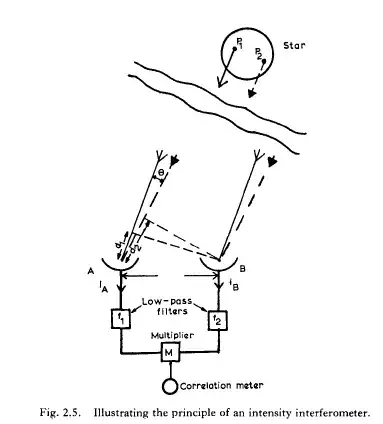
Let the emissions from points $P_1,P_2$ at a distant star be denoted by $$E_k \sin(\omega_k t+\phi_k);k=1,2\tag{1}$$ These emissions are received as uncorrelated white noise in a diode detector that behaves as a square-law detector for such low levels. There are two detectors, one for each antenna, $A$ and $B$. The diode current coming out of detector $A$ is
$$i_A=K_A[E_1 \sin(\omega_1 t+\phi_1)+E_2 \sin(\omega_2 t+\phi_2)]^2\tag{2}$$ for some $K_A$ characteristic of the detector circuit. The current of detector $B$ is similar but shifted in phase:
$$i_B=K_B[E_1 \sin(\omega_1 (t+d_1/c) + \phi_1)+E_2 \sin(\omega_2 (t+d_2/c)+\phi_2)]^2\tag{3}$$
After low pass and dc component filtering these can be written as
$$i^*_A=K_A E_1E_2[\cos(\omega_1-\omega_2)t+(\phi_1-\phi_2)]\\
i^*_B=K_B E_1E_2[\cos(\omega_1-\omega_2)t+(\phi_1-\phi_2)+\omega_1d_1/c-\omega_2d_2/c]\tag{4}$$
To correlate these two signal $i^*_A$ and $i^*_B$ these are multiplied and low pass filtered while assuming that $\omega_1\approx \omega_2 =\omega$, the remaining dc term is:
$$c=K_AK_BE^2_1E^2_2\cos[(\omega/c)(d_1-d_2)]\\
=K_AK_BE^2_1E^2_2\cos(2\pi d\theta/\lambda)] \tag{5}$$
where $d$ is the distance between the two antennas and $\theta$ is the angle between the emitters and Eq (5) how it is measured by the correlation.