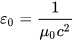Want to know about permittivity

Question

Why is the speed of light $c$ used to determine the value of permittivity in free space?

Answer 1

Why is the speed of light $c$ used to determine the value of permittivity in free space?

$$ \epsilon_0 = \frac{1}{\mu_0 c^2}\;. $$

This is a definition.

In SI units, Maxwell's equations can be reformulated into a wave equation (like $\frac{d^2\vec E}{dx^2}-\epsilon_0\mu_0\frac{d^2\vec E}{dt^2}=0$), where the parameter $\frac{1}{\epsilon_0 \mu_0}$ has units of speed squared. We call this speed $c$.

So, the squared speed is: $$ c^2 = \frac{1}{\epsilon_0 \mu_0} $$

Answer 2

The speed of light $c$ appears in this relation because of how the SI system of units is defined based on electromagnetic theory, where the permittivity and permeability of free space are:

$$\epsilon_0=\frac{e^2}{4\pi\alpha\hbar c} \qquad \mathrm{and} \qquad \mu_0=\frac{4\pi\alpha\hbar}{e^2c}$$

so

$$\epsilon_0 = \frac{1}{\mu_0 c^2}$$

This last relationship only depends on special relativity and is defined to be exact in the most recent update of the SI System of units. In the current SI system, the speed of light $c$, elementary charge $e$, and reduced Planck constant $\hbar$ all have defined values, so experimental measurements of $\epsilon_0$, $\mu_0$, or $\alpha$ are all equivalent. Direct macroscopic measurements of of $\mu_0$ or $\epsilon_0$, e.g. with a current balance or a parallel plate capacitor, are orders-of-magnitude less accurate than the best measurements of the fine structure constant $\alpha$, so the values $\epsilon_0$ and $\mu_0$ are calculated from the measured value of $\alpha$ and the defined values of $c$, $e$, and $\hbar$.

The answers to "Why does the vacuum even have permeability and permittivity?" are also relevant.