What is meant by precision of a measuring instrument?

Question

I came across many definitions of the precision of a measuring instrument such as, "a precise measuring tool is one that can measure values in very small increments" and "The precision of the instrument that is used to take a measurement is reflected in the smallest measure that the instrument can make". However, none of them provided precise information about what exactly is the precision of a measuring instrument?

Answer 1

Let me tell you one more way to interpret precision: it's a measure of an instrument's capability to reproduce the same readings during trials.

The term precision is used to describe the degree of freedom of a measurement system from random errors. Thus, a high precision measurement instrument will give only a small spread of readings if repeated readings are taken of the same quantity.(source)

There can be many ways to say the same thing but its essence remains unchanged. Here, the essence of the word precision is the ability to be precise. Precise comes from Latin "praecis-" ‘cut short’, it's how sharply an instrument can measure something. If a tool lacks precision, readings will vary with each trial, whereas a precise tool will generate identical readings most times.

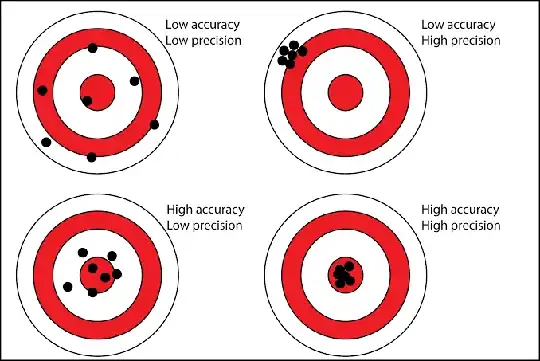
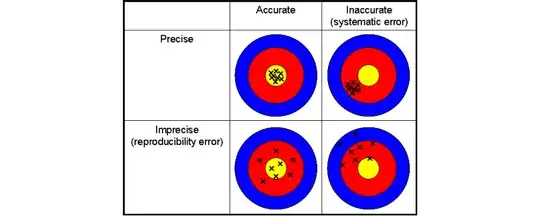
A precise instrument may or may not give correct readings. The ability to give correct measurements is called "accuracy". An accurate instrument may not be precise. Accuracy is often confused with precision; here is a good illustration:

Answer 2

I think quote

The precision of the instrument that is used to take a measurement is reflected in the smallest measure that the instrument can make.

says it all. Say you have such ruler (one of instruments) :

Then smallest length it can measure is $1~mm$ (omitting zero of course). Because ruler has no smaller scale ticks marked anymore, than 1 mm, hence this instrument system error is $\pm 1~mm$. When we measure length with this type of ruler we say that our obtained object length was $L \pm 1~mm$.

Sometimes system error is considered to be half of smallest measuring step. Consider that real object length is $0.5~mm$, however this ruler can't measure such small object, and so you are "forced" to choose $0 mm$ or $1mm$ value for an object length by applying this ruler measurement. And so you are "off" by $0.5mm$ from a real value. Hence you can state that your object length measurement error was $0.5mm$.

This is the rationale why sometimes system error of measuring instrument is considered $\frac 12 \Delta_{min}$ instead of simply device $\Delta_{min}$.

Answer 3

Thanks to the OP for the interesting question related to measuring physical quantities and metrics related to those measurements. Data sheets for sensors provide specifications based on metrics which can be diverse in definition. Understanding the relationship between the metrics is useful in experimental physics or engineering, and can help ascertain the intuition motivating the concepts of such metrics.

We present a brief but insightful comparative understanding of the most commonly used metrics to understand the limitations of sensors commonly studied by application of statistical metrics. Resolution, precision and accuracy are types of metrics or indicative classification classes of such metrics. A resolution metric expresses the smallest discernible difference or increment between two values that can be distinguished or resolved by a measurement or a system. An accuracy metric expresses how close a measured or observed value is to the true or actual value of a quantity. Usually, for any sensor, for a specific metric definition, the absolute resolution is lower than the absolute accuracy (error) or $$ \text{absolute resolution} < \text{absolute accuracy (error)} \\ \equiv \text{percentage absolute resolution} < \text{percentage absolute accuracy (error)}, $$ wherein the percentage absolute accuracy (error) or percentage absolute resolution refers to the ratio of the absolute values with the range of the sensor. Simply expressed, this means that we cannot be more accurate than the discrete quantity which we can measure. Indeed, in case of measurement of physical quantities by sensors this relationship is always true and it is difficult to come up with an example where this is not true.

In the context of sensors and measurements, precision refers to the degree of consistency or repeatability in a sensor's measurements when the same input or quantity is measured multiple times under similar conditions. Let's say we have a temperature sensor that, when exposed to the same temperature repeatedly, provides very similar output values each time. This indicates high precision. For instance, if the sensor measures a temperature of $25^o \; C$ and consistently outputs values like $250.1 \; mV, 250.2 \; mV$, and $250.0 \; mV$ over multiple measurements, it demonstrates high precision while if the sensor's output values for the same temperature vary widely such as $245.0 \; mV, 253.5 \; mV, 246.8 \; mV$ it suggests lower precision. Precision focuses on quantifying the consistency and reproducibility of measurements. A sensor that is precise produces similar measurements for the same input, indicating that it has low variability in its readings under similar conditions.

Overall, the absolute precision (error) is unrelated to the true measurement and is best described by the mean absolute deviation (MAD) or variance or standard deviation (STD) of the measurements while the absolute accuracy (error) is described by the mean absolute error (MAE) or root mean square error (RMSE) of the measurement relative to the true measurement. In practice, a sensor can be

• precise but not accurate (consistent but not necessarily correct),
• accurate but not precise (correct on average but with significant variability),
• both accurate and precise (consistent and correct),
• or neither accurate nor precise (inconsistent and incorrect).

The ideal situation is to have both accuracy and precision, ensuring measurements are both correct and consistent. The schematic below shows the distinction between these two metrics in the context of sensor measurements.