Normal Force and Newton's Third Law

Question

Normal force is the component of a contact force that is perpendicular to the surface that an object contacts.

Above is the Wikipedia definition of Normal Force. The confusion is regarding how the following scenario satisfies Newton's Third Law.

The scenario is:

A book is placed on a table and the following forces are involved :

1. Gravitational force by earth on the book.
2. Gravitational force by the book on earth.
3. Normal force by table on the book.
4. The push on the table by the book.

My confusion is that the force the book experiences due to gravity is the same force experienced by the table due to push from the book, same as in its the same force, not just the magnitude. So there are only three forces acting. There isn't action reaction pair for the normal force.

So, how does this work?

Answer 1

My confusion is that the force the book experiences due to gravity is the same force experienced by the table due to push from the book, same as in its the same force, not just the magnitude. So there are only three forces acting. There isn't action reaction pair for the normal force.

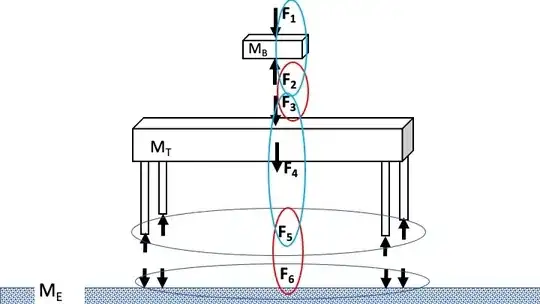
They are not the same force. See the free body diagrams (FBD) for the book and table below.

The force the book experiences due to gravity is $F_1$. It is not a contact force. In Newtonian mechanics it's a force experienced due to a field, in this case the local gravitational field. The force experienced by the table due to push from the book is $F_3$. It is a contact force (the result of electrical forces between atoms). The two forces happen to have the same magnitude only because the book is in equilibrium.

The forces shown in the FBD's are as follows:

$F_1$ = the force of gravity on the book = $M_{B}g$

$F_2$ = the normal force of the table on the book which, since the book is in equilibrium, = $M_{B}g$

$F_3$ = the normal force of the book on the table = $M_{B}g$

$F_4$ = the force of gravity on the table = $M_{T}g$

$F_5$ = the total normal force of the Earth on the table which, since the table is in equilibrium = $F_{3}+F_{4}=M_{B}g+M_{T}g$

$F_6$ = the total normal force of the table on the Earth = $F_{3}+F_{4}=M_{B}g+M_{T}g$

Not shown is the gravitational force that exists between the book and table. This force is infinitesimal compared to all the other forces.

The two Newton 3rd law equal and opposite forces pairs are $F_{2},F_{3}$ and $F_{5},F_{6}$, circled in red.

The forces acting on the book and the table for the application of Newton's 2nd law forces are circled in blue. The equilibrium requirements for the book and table are, respectively

$F_{1}+F_{2}=-M_{B}g+M_{B}g=0$

$F_{3}+F_{4}+F_{5}=-M_{B}g-M_{T}g+(M_{B}g+M_{T}g)=0$

Hope this helps.

Answer 2

My confusion is that the force the book experiences due to gravity is the same force experienced by the table due to push from the book, same as in its the same force, not just the magnitude.

This is false, and is leading to your confusion. It is not possible for these to be the same force for many reasons. The simplest reason is that the first force is applied to the book while the second is applied to the table. There's no way two forces can be "the same force" if they are applied to different objects. They happen to be the same magnitude and direction, but are not the same force.

The force of the book on the table (4), and the normal force the table pushes back on the book (3) are action-reaction pairs. They're actually not caused by gravity -- they are electrostatic repulsions between the electrons in the atoms of the table and book. If gravity were to magically vanish, this force would still be there and would actually accelerate the book upwards a little (the electrostatic forces would fall off over the course of picometers, but they would certainly cause an acceleration at the moment gravity vanished)

It happens to be that, in this case, many of the forces have the same magnitude and direction, such as (1) and (4). And all of the forces have the same magnitude. This is pure luck -- an artifact of this particular configuration of objects. It's trivial to come up with scenarios where the magnitudes don't happen to line up in this way.

Answer 3

It's easier to see what's going on if the table-top is made of a squashable material like foam-rubber.

If you place the book gently on the table the foam-rubber will deform and exert a larger and larger upward force ($\mathbf F_3$ using your numbering scheme) on the book. When the book comes to rest and you've let go of it, this fundamentally electromagnetic force will be large enough to balance the pull of the Earth on the book, that is $\mathbf F_3=-\mathbf F_1$ (equilibrium condition for book). The force exerted by the book on the table is the Newton's third law partner force to the force of the table on the book; $\mathbf F_3$ and $\mathbf F_4$ are manifestations of the same electromagnetic interaction, and $\mathbf F_3=-\mathbf F_4$

It follows from the two equations in the previous paragraph that $\mathbf F_4=\mathbf F_1$. But note that $\mathbf F_1$ is a gravitational force and $\mathbf F_4$ is electromagnetic (and that these forces act on different things).

Of course the same argument holds if the table-top isn't visibly squashable. A wooden table-top will deform when a book is placed upon it, but the deformation won't usually be seen.

Answer 4

In your scenario, the gravitational forces (1) and (2) are indeed an action/reaction force pair via Newton's 3rd law. (3) and (4) constitute another action/reaction force pair via Newton's 3rd law.

In general, these two pairs do not have to have anything to do with each other. Gravity and normal forces do not have to be tied together in any way. In your scenario, (1) and (4) do happen to be identical, yes, but that is not a general rule; that is just your chosen special case.

• Place a stone on the book. (4) is now larger and no longer identical to (1) since it now must hold back against two gravitational forces.

• Or push the book off the table into a free fall. (4) is now zero while (1) hasn't changed.

• Or lift the book up and slam it onto the table. (4) is now much greater than (1) since it acts against the gravitational force while also causing deceleration.

It often is the case that gravity and normal force are linked. But mainly in text books, that is. That might be the reason for why this misconception is common. Your scenario is a typical text-book idealisation. There is no law always tying them together as a general rule, as the examples above show.

Answer 5

"Push on the table by the book." said force in your question is gravitational force, between the earth and the book, with a magnitude equal to its weight $mg$. The normal by the table is due to Newton's Third Law. And the gravitational forces between the book and table themselves, usually so small in magnitude that they're considered negligible, are a pair of action reaction forces as well.