disclaimer: This post is about a proton electric dipole moment, but it might be the case that the proton electric quadrapole moment is known to be non-zero..
I don't know the physics of quarks and gluons, but I know some basic electric theory and some experimental physics.
The potential from some source charge near the origin can be written as
$$
V(r, \theta, \phi) = \sum_{j=1}^{\infty}\sum_{\ell=0}^{\infty}\sum_{m=-\ell}^{+\ell} \frac{D_{\ell, j}^m}{r^j} Y_{\ell}^m(\theta, \phi)
$$
By symmetry, if the charge distribution $\rho(r, \theta, \phi)$ is spherically symmetric then the only terms $D_{\ell, j}^m$ with $\ell, m=0$ will contribute. These are the monopole terms. The first order deviation from spherical symmetry would be the inclusion of a dipolar terms with $\ell=1$.
"The storage ring proton EDM experiment" describes an experiment looking for an electric dipole moment of the proton. I do not know how this experiment works, but I can copy and paste this figure and its caption.
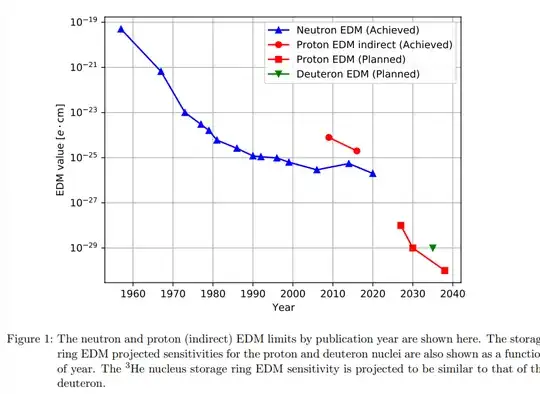
This figure shows that we have never observe an electric dipole moment of the proton, but that it has been constrained to be $d<10^{-24}\text{ e}\cdot\text{cm}$.
Here's a comparison I have to put that number into perspective. In atoms the radius of the electron cloud is the Bohr radius $\approx a_0 \approx 50 \text{ pm}$. When electrons in atoms are driven between the $S$ and $P$ orbitals there is an associated dipole moment of a scale $d\approx e\cdot a_0$. That is, the length scale of the dipole moment is as large as the radius of the charge distribution.
Apparently the charge radius of the proton is $\approx 1 \text{ fm} = 10^{-13}\text{ cm}$. The length scale of the proton dipole moment has been constrained be 11 orders of magnitude smaller than this. What that tells me as a naive experimentalist is that if the proton is made of multiple components then, for whatever reason, those components occupy orbitals that are HIGHLY spherical.
