Let me show you some details about this question.
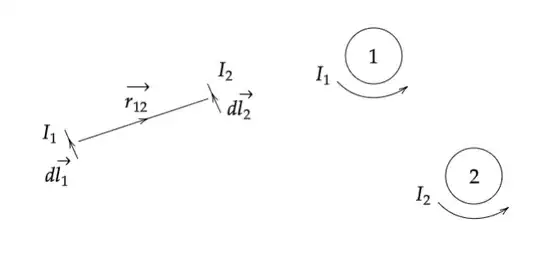
As the left part of the above picture shows: the magnetic field that 2 gives 1 can be written as:
$$
B_{12}=\frac{\mu_0}{4\pi}\frac{I_1d\vec l_1\times\vec {r_{12}}}{r_{12}^3}
$$
And the force which $I_2$ feels is
$$
d\vec F_{12}=I_2d\vec l_2\times B_{12}=\frac{\mu_0I_1I_2}{4\pi}\frac{d\vec l_2\times(d\vec l_1\times\vec {r_{12}})}{r_{12}^3}
$$
Same for $I_1$
$$
d\vec F_{21}=I_2d\vec l_2\times B_{12}=\frac{\mu_0I_1I_2}{4\pi}\frac{d\vec l_1\times(d\vec l_2\times\vec {r_{12}})}{r_{12}^3}
$$
The direction of $dF_{12}$ and $dF_{21}$ is
$$
(d\vec{l_2}\cdot\vec r_{12})d\vec {l_1}-(d\vec l_1\cdot d\vec l_2)\vec r_{12}
$$
and
$$
(d\vec{l_1}\cdot\vec r_{21})d\vec {l_2}-(d\vec l_2\cdot d\vec l_1)\vec r_{21}
$$
Apparently not in same line, which means doubt in Newton's Law. But just like @Philip Wood said, in real world, always complete circuit like the right part of the picture. So we consider the whole loop.
Take $F_{12}$ as the example
$$
F_{12}=\iint dF_{12}=\frac{\mu_0I_1I_2}{4\pi}\oint_{L_1}\oint_{L_2}\frac{(d\vec{l_2}\cdot\vec r_{12})d\vec {l_1}}{r_{12}^3}-\frac{(d\vec l_1\cdot d\vec l_2)\vec r_{12}}{r_{12}^3}
$$
The first term can be written as
$$
\oint_{L_2}\frac{d\vec{l_2}\cdot\vec r_{12}}{r_{12}^3}=\oint\frac{d\vec r \cdot\vec r}{r^3}=\oint\frac{d\vec r}{r^2}=0\ (\text{because of the loop integrate})
$$
So only the second term will be remained. For the second terms, it's clear that $\vec F_{12}$ and $\vec F_{21}$ obey Newton's 3rd Law.
Hope my answer can help u!
