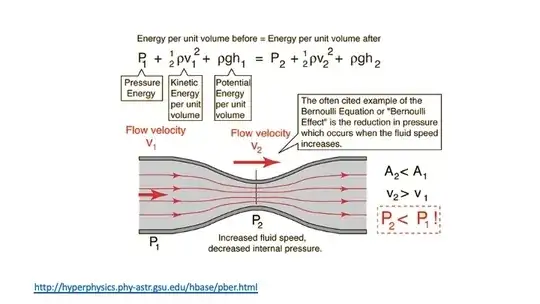
You are correct - the pressure term in Bernoulli's equation is not some kind of additional energy density contribution; it is just pressure. Calling $p$ "pressure energy" or "pressure energy density" is a misconception based on an attractive, widespread and wrong interpretation of the Bernoulli equation.
This wrong interpretation goes like this. The Bernoulli equation is
$$
\frac{1}{2}\rho v^2 +\rho g h + p = const.
$$
This is a sum of terms with units of energy density, so the equation looks like it could be an equation of conservation of energy, if only the left-hand side was the total energy of the fluid. Intuitively we accept that increasing pressure in practice takes work, so without deep thought, we tend to call the term $p$ "pressure energy", and the misconception is born.
The problem with the intuition is, it takes zero work to increase pressure of a fluid element in this case, because we are dealing with incompressible flow. The element of fluid does not change its volume at all, and thus no work is consumed to increase pressure in it, even though pressure may increase during its motion.
The left-hand side is therefore not the total energy density of the fluid. Total energy in mechanics (including mechanics of incompressible fluids) is sum of kinetic and potential energy. For incompressible fluid in gravity field, density of total energy is sum of density of kinetic energy and density of potential energy:
$$
e = \frac{1}{2}\rho v^2 +\rho g h.
$$
Where does does the Bernoulli equation come from then, if it is not a statement of conservation of energy?
It may be derived in different ways, e.g. from the Euler equation which is a form of Newton's equation $\mathbf F=m\mathbf a$ adapted to fluids. But the simplest derivation is from the variant of a work-energy theorem applied to the fluid element. This theorem (in contrast to the idea of conservation of energy of the element) says that kinetic energy of the fluid element changes as it undergoes a displacement, proportionally to net work of all forces acting on the element.
This can be adapted to the formulation: total energy of the fluid (kinetic energy + potential gravitational energy) changes in proportion to net work of the pressure forces. It is the work of the pressure forces which introduces the pressure term $p$ into our equation.
Let us consider a fluid element in shape of a cylinder, with its axis aligned with the flow. Let us consider a small displacement $\Delta x$ along its axis (much smaller than the cylinder length), while pressure force $p_1A$ acts on the back face (1 refers to the back face), and pressure force $-p_2A$ acts on the front face (2 refer to the front face). After the displacement, volume $A\Delta x$ of the element gets into a new region of the flow (near the front face of the cylinder) where total energy density is $e_2 = \frac{1}{2}\rho v_2^2 + \rho g h_2$, and the same volume is removed from the region where it had total energy density $e_1 = \frac{1}{2}\rho v_1^2 + \rho g h_1$ (near the back face of the cylinder). Thus increase of total energy of the cylinder is
$$
A\Delta x \bigg(\frac{1}{2}\rho v_2^2 + \rho g h_2\bigg) - A\Delta x \bigg(\frac{1}{2}\rho v_1^2 + \rho g h_1\bigg).
$$
Net work done by external pressure forces during this displacement is
$$
A (p_1 - p_2) \Delta x.
$$
Since change of energy equals this work, we have
$$
\bigg(\frac{1}{2}\rho v_2^2 + \rho g h_2\bigg) - \bigg(\frac{1}{2}\rho v_1^2 + \rho g h_1\bigg) = p_1 - p_2.
$$
Since we can imagine such cylinder anywhere on the streamline, the equation holds for any pair of points on the streamline. Denoting
$$
\frac{1}{2}\rho v_1^2 + \rho g h_1 + p_1 =C
$$
we can simply restate that for any point on the streamline, velocity $v$, height $h$ and pressure $p$ obey the equation
$$
\frac{1}{2}\rho v^2 + \rho g h + p =C.
$$
The pressure term comes from the expression of work on the fluid element; it does not come from expression of total energy of the fluid element.