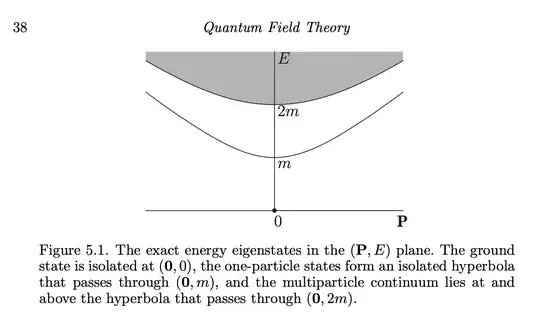
In Peskin & Schroeder, equation (7.2), I found this completeness relation for the momentum eigenstates $|\lambda_p\rangle$:
$$\mathbf 1=|\Omega\rangle\langle\Omega|+\sum_\lambda\int\frac{d^3p}{(2\pi)^2}\frac{1}{2E_{\mathbf p}(\lambda)}|\lambda_\mathbf p\rangle\langle\lambda_{\mathbf p}|.\tag{7.2}$$
Here $|\Omega\rangle$ is the vacuum, and $|\lambda_p\rangle$ represents the state with one particle labeled by $\lambda$ with momentum $p$. The $\lambda$ sum is over all types of particles in the theory. I can understand why we sum over all $\lambda$. However, I do not understand why we have to integrate state $\lambda_p$ over momentum space?