At long distances QCD is said to give rise to attractive force between nucleons by pion exchange and to give rise to repulsive force at short distance mediated by vector mesons. Is there a quantitative explanation and derivation of this somewhere? All seems to be rooted in ancient and cryptic material from the 70s that these days requires an archeologist to decipher. Is the nature of pion as pseudo-scalar (instead of scalar) relevant for this? What if the $\rho$ where a pseudo-vector instead of a vector?
1 Answers
Indeed, the VDM model of the 60s described photon-hadron interactions at low energy quite well, where only lattice QCD can provide "just so" answers today.
Today's chiral lagrangians for soft physics provide a very successful framework for fits, and confirm the VDM. The vector dominance idea has never been derived from the Standard Model, but nevertheless enjoys considerable phenomenological support.
Quoting from Ch VII-4 of DYNAMICS OF THE STANDARD MODEL , of J Donoghue, E Golowich, & B Holstein, Cambr Univ Press,
Finally, it also turns out that the use of vector meson exchange leads to a good description of ππ scattering. This is not too surprising in light of the need for the chiral lagrangians to reproduce the tail of the ρ(770), as described in Sect. VII–3. As a consequence of crossing symmetry, the ρ(770) must also influence the other scattering channels. To a large extent, the chiral coefficients L1,L2,L3 are dominated by the effect of ρ(770) exchange. We see from these examples that phenomenology indicates that the exchange of light vector particles is the most important physics effect behind the chiral coefficients which we have been discussing. The idea that vector mesons play an important dynamical role is not new. It pre-dates the Standard Model, originating with Sakurai, in a form called vector dominance. Put most broadly, vector dominance states that the main dynamical effect at energies less than about 1 GeV is associated with the exchange of vector mesons. The use of a chiral lagrangian with parameters described by ρ-exchange, is compatible with this idea and puts it on a firmer footing. These considerations suggest that for chiral lagrangians the prime ingredient of QCD is the spectrum of the theory. The linear sigma model has a quite different spectrum, with a light scalar and no ρ, and. hence does not agree with the data. QCD, however, seems to predict that deviations from the lowest-order chiral relation must be in such a form as to reproduce the low-energy tails of the light resonances, in particular the ρ. At present, we cannot rigorously prove this connection. However, it remains a useful picture in estimating various effects of chiral lagrangians.
Now, you seem to be also making a separate, mysterious garbled connection to the vector meson exchange contributions to nuclear potentials, which is unrelated, to my mind, at this stage.
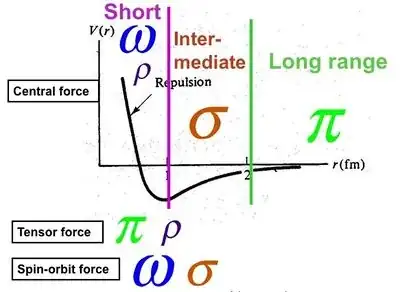
As you have probably learned, spinless particles (of either parity) provide attractive forces, like the σ in the nucleus, or the π when the tensor features of the scattering can be ignored. Likewise, vectors or axial vectors are entwined by charge conjugation, so, like the photon, may provide either attractive, or repulsive interactions, again, if the tensor and isospin structure can be ignored--rarely. (NB: the graviton, of spin 2, may only provide an attractive force like the spinless mesons. There are numerous questions and answers on this site fleshing out the point.)
Post Q Edit edit : As it became alarmingly apparent, VDM is not the core of your question, or, as indicated above, not even relevant. There are ample discussions on this site on the connection between the spin of mediators to the attractiveness/repulsiveness of the classical limit force, such as this; this; this; this; this, and links thereto. Perhaps you might ask a different question without VDM...
- 67,623