Double slit diffraction integral?

Question

In our physics class, the professor went over a so-called "diffraction integral" for single slit diffraction:

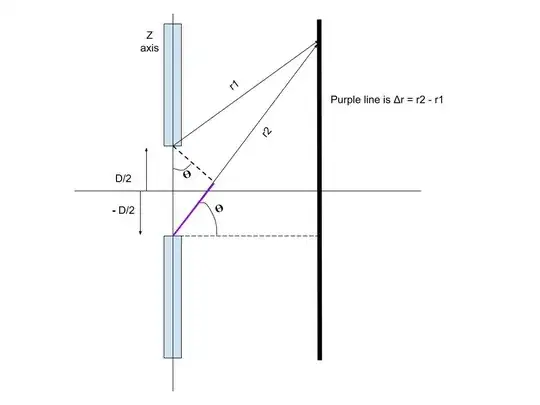
$$E = E_0\cos(kx - kct)\qquad\text{then we ignore time dependence}:$$ $$E = E_0\cos(kx)$$ $$\Delta E = E_0 \cos(k\Delta r)$$ $$\Delta E = E_0 \cos(k\sin(\theta)z)$$ $$E = \frac{1}{D} \int_{-D/2}^{D/2} E_0 \cos(k\sin(\theta)z) dz$$ $$E = E_0 \frac{2\sin(k\sin(\theta)D/2)}{k\sin(\theta)D}$$ $$E = \text{sinc}(k\sin(\theta) \frac{D}{2})$$

Can we set up and evaluate such an integral for double slit diffraction? I tried doing so, but I got an answer that doesn't match the commonly accepted equation for double slit diffraction. That commonly accepted equation is $$E = \text{sinc}(k\sin(\theta) \frac{D}{2}) \cos(k\sin(\theta) \frac{D}{2})$$

Any help would be much appreciated. For reference, I've already seen and read the post: Double slit diffraction derivation, and did not understand very much because it uses physics that we haven't been taught yet, like Fraunhofer diffraction.

Answer 1

Yes you can. For years, I devoted my efforts to exploring more efficient and straightforward methods for deducing fringe patterns in various slit experiments. I discovered a significantly simplified approach by computing from the individual edges of the slits. This method enables the calculation of even a single edge's fringe pattern.

In the case of a single slit, there are two edges separated by a specific distance, and the diffraction pattern for each edge can be easily determined. Overlaying these two patterns results in the characteristic pattern of a single slit. Similarly, for double-slit patterns, four identical single-edge calculations are overlaid to generate a two-slit pattern.

The equations involved are remarkably straightforward, allowing me to develop simulators for edge, single slits, and multiple slit patterns. You can access these simulations on my website, billalsept.com, by scrolling down to the sections labeled 1Edge, 2Edge, 4Edge, etc. These simulations are Excel-based and user-friendly. I explain how I developed the simulators in my paper "Single Edge Certainty" also on my website.