Help Understanding Spontaneous Alpha Decay

Question

I've been reading through my Physics textbook (College Physics 2e on OpenStax) and I'm a bit confused by how it explains when alpha decay is spontaneous. Here is the quote for context:

When the final products have less total mass, Δm is positive, and the reaction releases energy (is exothermic). When the products have greater total mass, the reaction is endothermic (Δm is negative) and must be induced with an energy input. For α decay to be spontaneous, the decay products must have smaller mass than the parent.

Considering the fact that the final decay products are a helium nucleus and the parent nuclide minus two protons and two neutrons (i.e., a helium nucleus), wouldn't the final products of decay always have the same total mass as the parent nuclide? In what circumstances would the decay products be less massive than the parent nuclide? I feel like I must be missing something, so help is greatly appreciated.

Answer 1

As others have mentioned, the answer is indeed binding energy. I suggest you perform your own research on it, but here is a brief summary of what it is and why it is so important in nuclear physics.

Binding energy is essentially the energy required to separate the elements of a system which are being held together by an attractive force. Systems that are tightly bound require more energy to separate and thus have a greater binding energy. When systems transition between states with greater or lesser binding energies, the difference in binding energy must be released or absorbed by the system, respectively. For example, if a positive and negative charge are very far apart, the attractive force between them is quite weak. It is therefore easy to separate them and their binding energy is low. However, as they accelerate towards each other, they transition into a state with greater binding energy, as when they are close together, the attractive force is much stronger and therefore they require more energy to separate. The difference in binding energies is released, in some sense, as the kinetic energy of the charges as they accelerate towards each other.

In nuclear physics, the binding energies we care about are due to the strong nuclear force, which is attractive. Here is a graph of the binding energy per nucleon versus the number of nucleons.

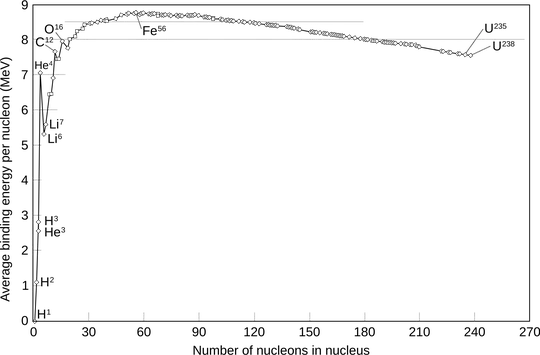
As can be seen, past iron, the lighter the nucleus, the greater the binding energy. So when a nucleus heavier than iron emits an alpha particle, it becomes lighter and thus more tightly bound, so its binding energy increases. It thus must release energy. Since energy is mass and mass is energy, this means that the total mass of the products is less than the total mass of the initial nucleus. This is why the total energy released or absorbed by a nuclear reaction (or really, any reaction, but it is only in nuclear reactions where this is significant) can be calculated by multiplying the difference in masses by the speed of light squared.