If I have a block of let's say: 10 kg and I put it over my foot in a static manner, what we know from static mechanics is that my foot is opposing the weight of the 10 kg mass with the same force in opposite direction to maintain equilibrium, which would be around 100N. Now let's add some motion, and drop the 10 kg over a height of 30 cm for example. Why is my foot getting crushed? Isn't the same 100N of force I just withstood with ease in the static example? I know the object has more potential energy now but I can't wrap my head around the fact that the weight isn't changing and I am reacting with and opposing force of 100N in both cases. If the force is the same why the presence of height "adds" more weight. How can we explain this from a pure dynamic/kinematics perspective without using conservation of energy arguments?
6 Answers
Your foot brings the falling block rapidly to rest. Suppose the block has been dropped from a height of 0.90 m above the top of your foot. When it reaches the top of your foot it will be falling at 4.2 m s$^{-1}$. Your foot is fairly unyielding and will bring the block to rest in a very short time – say 0.10 s. The block's mean deceleration (that is its upward acceleration) will therefore be
$$\text{acceleration} = \frac{\text{change in velocity}}{\text{time taken to change}} =\frac{0-(-4.2)\text {m s}^{-1}}{0.10\ \text s} = 42\ \text{m s}^{-2}.$$ The mean upward force on the block during this deceleration will be
$$\text{Net force} = 10\ \text{kg} \times 42\ \text{m s}^{-2} = 420 \ \text{N}. $$
But the net force on the block is the upward force from your foot minus the pull of the Earth.
Therefore your foot must exert a force of 420 N + 98 N = 520 N (2 sig figs) on the block. Your foot will therefore, according to Newton's third law, experience a mean downward force of 520 N from the block. When the block has reached equilibrium it will exert a mere 98 N on your foot.
- 37,325
When the dropped block hits your foot, it has a certain amount of momentum, p. A force F(t) must be provided over a time interval to bring it to rest, where $\int F(t)$dt = p. The smaller the time interval, the larger the maximum force Fmax required. You have to apply Fmax + mg, to take account of the downward force of gravity, and it is that sum of forces that the block will exert on your foot. That sum is > mg.
Edited upon reading answer from @Philip Wood to take account of the block's weight.
- 2,816
Weight is the force that the earth does on the block. It doesn't change if it is falling or not.
But the force that the block does on your feet is a different matter. If it is just there in a static equilibrium, it happens to be the equal to the weight.
But if it hit the feet after falling down, the feet does a force to decelerate its velocity to zero. That force depends on the instantaneous velocity of the block at the impact, and the time (crunching the flesh and bones) to stop. The feet obviously suffer the same force by the Newton's third law.
- 17,607
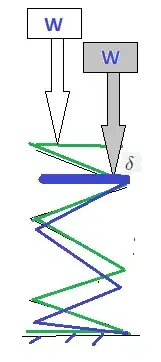
After falling from height $h$ and impacting elastically with the spring (of constant k) the weight W and top part of spring travel down together by a common deflection $\delta$.
Equating work done to potential energy
$$ \frac12 k ~\delta^2= W(\delta+h) $$
$$\delta^2 -\frac{2W \delta}{k}-\frac{2Wh}{k}=0$$
The solution of quadratic with proper sign
$$ \delta= \frac{W}{k} +\sqrt{\left(\frac{W}{k}\right)^2 + \frac{2Wh}{k}}$$
The result shows that even though $h=0$ ( true for a slowly introduced load) the effective deflection and in effect the force by load is double that of static load $ \dfrac{W}{k}$. It is even more when $h>0$.
- 1,142
A true causation for your demonstration relies in the concept of Impulse. Discarding the conventional answer, if you want to go far beyond and evaluate the truth see https://www.researchgate.net/publication/323316385_A_new_course_of_relative_acceleration_within_Classical_regime .
The answer is very simple. When a body is dropped from a certain height, the quantity of motion is involved. Another name for quantity of motion is linear momentum. The change in linear momentum is equal to impulse. Impulse is nothing but a large force acting for a short period of time. The impulse or impact is the cause for foot being crushed.
- 93