Sending photons in opposite directions in a closed universe leads to different proper time before we see them again?

Question

Consider a closed universe that's a 1D circle with circumference of $30$ light years in an inertial reference frame that we'll call $C_1$.

This universe has an observer who is travelling at a constant speed of $3/5c$ to the right according to our first reference frame and nothing else. Since they're not accelerating they are also in an inertial reference frame which we'll call $C_2$.

To measure the circumference of the universe for themselves, they send a photon in one direction and measure the proper time they experience it takes for the photon to come back. Since the photon always travels at speed $c$ regardless of reference frame they know that if it takes $k$ years to see the photon again the universe must have circumference $k$ light years for them. We'll say the observer is at coordinate spacetime of $(x,t) = (0,0)$ according to $C_1$ when they send the particle.

I drew a spacetime diagram to calculate what this proper time should be, but I am getting different answers based on whether the observer sends the particle in the same direction that they are moving or the opposite direction.

Note that for the observer themselves they are at rest so don't have any preferred direction for sending the particle, all they see is that they send it in one direction and eventually it comes back to them from the opposite direction:

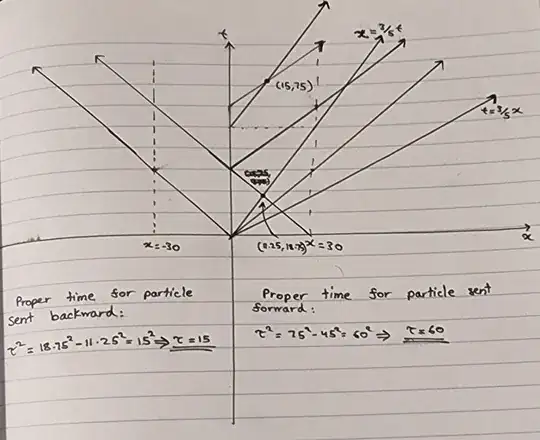
If the photon is sent in the opposite direction to the observer, then the observer first meets the particle at coordinate spacetime $(x,t) = (11.25,18.75)$ in the frame $C_1$ which we get from solving the pair of equations $x = 3/5t; x = 30-t$ (with the photon wrapping around once). This leads to a proper time observed of $\tau^2 = t^2-x^2 = 18.75^2-11.25^2 = 15^2$ so $\tau = 15$ and our observer thinks the universe has circumference $15$ light years.

If the photon is sent in the same direction as the observeris moving according to $C_1$ then the equations to solve are $x=3/5t; x=t-30$ and so the observer first meets the particle at coordinate spacetime $(x,t) = (45,75) \cong (15,75)$ where the observer makes one complete circumnavigation of the universe and the photon two of them and the proper time experienced by the observer is $\tau^2 = t^2-x^2 = 75^2-45^2 = 60^2$ so $\tau = 60$ and our observer considers the universe to have a circumference of $60$ light years.

I don't understand what makes it possible for these answers to be so different here where we have a factor of 4 difference in the universe size according to the observer based on whether they send the particle to the left or the right, what am I missing here?

Also, if I just use the standard length contraction formula (e.g. assume there is a big ruler in the universe which in $C_1$ has a length of 30 light years), then I get that in $C_2$ the circumference of the universe should be $L_0\sqrt{1-v^2/c^2} = 30 \times 4/5 = 24$ light years, which is a different answer to both the other ones...

Answer 1

If the circumference in the frame of a comoving FLRW observer who observes no dipole in the CMB was x lightyears, the circumference in the frame of an observer travelling with v relative to the comoving observer will be lorentzcontracted by √(1-v²/c²) in the direction of motion.

The comoving observers are those with the longest possible proper time since the big bang, which is also the case in an infinite universe without spatial curvature.

In a static and closed universe without a CMB background you can send lightrays in opposite directions and wait to find out if they arrive back at you simultaneously. If so you are in the preferred frame with the longest possible proper time, and you will be the oldest twin in the general relativistic twin paradox.

Answer 2

Nothing in this problem depends essentially on the spacetime signature, so consider instead a Euclidean cylinder, which you might take to be the subspace of $\mathbb R^3$ (with standard Euclidean metric) satisfying $x^2+y^2=R^2$ where $R=15/π$ light years. What's the circumference of this cylinder? It's obviously $2πR = 30$ light years, but let's try to complicate the issue.

You can put $(w,z)$ coordinates on the cylinder where $x+iy = R e^{iw/R}$. Any line of the form $z=\text{const}$ has a length of $2πR$. This is another way of expressing the fact that the circumference is $2πR$.

If that's too simple, you could consider the lines $w=\pm mz$, which intersect $w=0$ at $z\in (2πR/m) \mathbb Z$. Measure the difference between adjacent points of intersection, multiply by $m$, and you have the circumference again. This is analogous to measuring the circumnavigation time of a test particle with a velocity of $m$ relative to $C_1$.

If that's too simple, instead of looking at the intersections of $w=\pm mz$ with $w=0$, you could look at the intersections of $w=\pm mz$ with $w=m'z$, which occur at $z$-intervals of $2πR/(m'\pm m)$, or length intervals along $w=m'z$ of $2πR/γ(m'\pm m)$ where $γ=1/\sqrt{1+m'^2}$. This depends on the sign of $\pm m$ unless $m'=0$, so you'll get different raw numbers depending on which way you send the test particle.

The number of ways in which you might measure or characterize the circumference is open-ended, but at any rate the cylinder has a circumference whose value doesn't depend on how you measure it.

The spacetime in your question differs from this cylinder only in being a subspace of $\mathbb R^{2,1}$ instead of $\mathbb R^3$. None of the philosophical issues of interpretation are different either. The spacetime has a well-defined circumference that you can measure in various ways. If you get a value other than 30 light years, then you didn't measure the circumference. What you measured may be interesting in its own right, or it may be the length of some random line segment in some compass-and-straightedge construction of no particular interest.

Everything that they say in introductory textbooks about "observers disagreeing about properties of the universe" is lies to children. The physical reality is the spacetime manifold and its intrinsic geometry, which everyone agrees on. "Observers" are just coordinate systems, and they disagree with each other only in the sense that coordinates in different coordinate systems are different.

Answer 3

The chart map that you have used does not cover the entirety of the spacetime because the underlying (1+1)D manifold's global topology is $\mathbb{R}\times\mathbb{S}$ while the topology of the chart is $\mathbb{R}\times\mathbb{R}$. A chart map that fully covers such a manifold cannot exist as that goes against the definition of chart maps since they land in $\mathbb{R}^d$ ($d = 2$ here).

But you identify the endpoints of the chart to make the $\mathbb{R}$ into a compact set. But this then does not remain a chart anymore in the usual definition of the chart of a topological manifold. Moreover, this identification of the endpoints is not universally agreed upon due to the relativity of simultaneity, as @Michael Seifert also points out.

As a result, the frame $C_2$ would see the geodesic jump in the time direction at the gluing boundary (forward in time for the right-going beam and backward for the left-going one) where the gluing is done by frame $C_1$. As such, the geodesic motion becomes discontinuous w.r.t. $C_2$.

Answer 4

The metric for rotating reference frame is:$$ ds^{2}=\left(c^{2}-\omega^{2}r^{2}\right)dt^{2}-2\omega r^{2} d\phi dt-dr ^{2}-r ^{2}d\phi ^{2}\;\;\;\; \,(*)$$ with $\;r\omega=v$

As in any stationary field, clocks cannot be uniquely synchronized at all points of a rotating body. Synchronizing along a closed contour, we obtain, once returned to the starting point

$$\left(1-\beta^{2}\right)c^{2}dt^{2}-2vdSdt-dS^{2}=0$$ ($dS=rd\phi$:arc of the circle,$\;\;,dr=0$ ) $$\Delta = 4dS^{2}$$ $$cdt_{+}=\frac{dS}{1-\beta}\;,\;cdt_{-}=-\frac{dS}{1+\beta}\;\;,\;\;\beta=v/c$$

i.e. $$ct_{+}-vt_{+}=S\;,\;ct_{-}+vt_{-}=S$$

$$x_{+}=ct_{+}-S\;,\;x_{-}=S-ct_{-} $$ so the metric contains both cases at the same time:$$S^{2}=c^{2}\tau^{2}=(ct_{+}-vt_{+})(ct_{-}+vt_{-})=(1-\beta^{2})c^{2}t_{+}t_{-}=(1-\beta^{2})c^{2}t'^{2}$$ with: $\;\;t'^{2}=t_{+}t_{-}=\gamma^{2} \tau^{2}$

the same as for the Michelson-Morley experiment

$$L^{2}=x^{2}=(ct'_{1}-vt'_{1})(ct'_{2}+vt'_{2})=(1-\beta^{2})c^{2}t'_{1}t'_{2}=(1-\beta^{2})c^{2}t'^{2}$$ with intermediate transformations:$$\begin{cases}x=x'_{1}-vt'_{1}\\x=x'_{2}+vt'_{2}\end{cases}$$ i.e. \begin{cases}x'_{1}=x+\frac{vt}{1-\beta}\\x'_{2}=x-\frac{vt}{1+\beta}\end{cases}

which can be demonstrated by another, simpler approach.

(*)How do I transform onto a relativistic rotating frame of reference? https://en.wikipedia.org/wiki/Born_coordinates https://en.wikipedia.org/wiki/Sagnac_effect